DTMerのためのデジタル信号処理 ~IIRなEQを作ろう~
Published: 2025-03-16
はじめに
こんにちは!Kashiwadeです。普段はオーケストラ系の曲を作っています。
最近円安で辛いですね…。全然プラグイン買えてないです。プラグインを買えないなら…自作してしまいましょう!!というわけで過去何回かプラグイン自作記事を書いてきました。JUCEを使うと簡単にプラグインを作ることができます。
もちろんEQも簡単に作れます。JUCEにはめっちゃ便利なクラス があるので、これにサンプルを渡すだけでEQをかけれます。
でも、折角プラグインを自作するならこだわりたいですよね…?肝心要の信号処理部分は自分で1から練り上げたものを使いたいですよね…?
というわけでこの記事では、デジタル信号処理の基礎と、IIR型のEQの原理と実装方法を説明します!ライブラリに頼らずIIRなEQを自作プラグインに組み込めるようになりましょう!
元々は自分の勉強用に書いていたメモを、外部公開用にアップデートした感じの記事です。なので、以降の本文は文体が固くなります。
この記事には間違いがあるかもしれません!もし間違いがあったら教えてください!!!
目次
Chapter 1. 前提知識
本文を理解するうえで必要な前提知識を浚う。
よく使う文字の定義
j j j j 2 = − 1 j^2=-1 j 2 = − 1 j j j
普通はi i i I I I j j j
k k k n n n ω \omega ω ω \omega ω オイラーの公式
信号解析で頻出の「複素数乗」とは一体なんなのかを理解する必要がある。
e j x = cos x + j sin x e^{jx} = \cos x + j \sin x e j x = cos x + j sin x 直感的な証明
e x e^x e x
e x = ∑ n = 0 ∞ x n n ! e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} e x = n = 0 ∑ ∞ n ! x n 実はx x x
e j x = ∑ n = 0 ∞ ( j x ) n n ! = ∑ n = 0 ∞ j n n ! x n = ∑ k = 0 ∞ j 2 k ( 2 k ) ! x 2 k + ∑ k = 0 ∞ j 2 k + 1 ( 2 k + 1 ) ! x 2 k + 1 = ∑ k = 0 ∞ ( − 1 ) k ( 2 k ) ! x 2 k + j ∑ k = 0 ∞ ( − 1 ) k ( 2 k + 1 ) ! x 2 k + 1 \begin{aligned}
e^{jx} &= \sum_{n=0}^{\infty} \frac{(jx)^n}{n!} = \sum_{n=0}^{\infty} \frac{j^n}{n!}x^n \\
&= \sum_{k=0}^{\infty} \frac{j^{2k}}{(2k)!}x^{2k} + \sum_{k=0}^{\infty} \frac{j^{2k+1}}{(2k+1)!}x^{2k+1} \\
&= \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k)!}x^{2k} + j \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k+1)!}x^{2k+1} \\
\end{aligned} e j x = n = 0 ∑ ∞ n ! ( j x ) n = n = 0 ∑ ∞ n ! j n x n = k = 0 ∑ ∞ ( 2 k )! j 2 k x 2 k + k = 0 ∑ ∞ ( 2 k + 1 )! j 2 k + 1 x 2 k + 1 = k = 0 ∑ ∞ ( 2 k )! ( − 1 ) k x 2 k + j k = 0 ∑ ∞ ( 2 k + 1 )! ( − 1 ) k x 2 k + 1 ちなみに、
cos x = ∑ n = 0 ∞ ( − 1 ) n ( 2 n ) ! x 2 n sin x = ∑ n = 0 ∞ ( − 1 ) n ( 2 n + 1 ) ! x 2 n + 1 \begin{aligned}
\cos x &= \sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2n)!}x^{2n} \\
\sin x &= \sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2n+1)!}x^{2n+1}
\end{aligned} cos x sin x = n = 0 ∑ ∞ ( 2 n )! ( − 1 ) n x 2 n = n = 0 ∑ ∞ ( 2 n + 1 )! ( − 1 ) n x 2 n + 1 なので、
e j x = cos x + j sin x e^{jx} = \cos x + j \sin x e j x = cos x + j sin x を得る。
オイラーの公式の嬉しさ
オイラーの公式の嬉しさを説明する為に、複素数平面の嬉しさを説明する。
複素数平面とは、横軸に実軸(Reと書くことが多い)、縦軸に虚軸(Imと書くことが多い)をとった平面である。通常の二次元平面では点Aの座標を( 1 , 2 ) (1, 2) ( 1 , 2 ) 1 + 2 j 1+2j 1 + 2 j j j j j 2 = − 1 j^2=-1 j 2 = − 1 j j j
従来であれば1つの点の位置を表現するのに2つの値が必要だったが、複素数平面を用いることで、1つの点の位置を表現するのに1つの値で十分になる。
続いて、オイラーの公式の両辺にA A A A e j x = A cos x + j A sin x Ae^{jx} = A \cos x + j A \sin x A e j x = A cos x + j A sin x
複素数平面なら1つの点の位置を表現するのに1つの値で十分になるという意味が明白になったと思う。
フーリエ変換
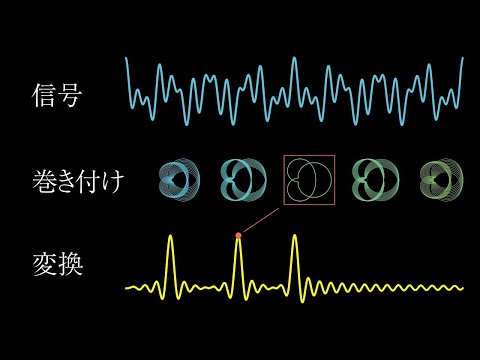
下記の動画が分かりやすい。信号を単位円上に巻きつけて、それの重心を考えるというアイデアである。
この結果、連続的な信号f ( t ) f(t) f ( t )
F [ f ( t ) ] ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t \mathcal{F}[f(t)](\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt F [ f ( t )] ( ω ) = ∫ − ∞ ∞ f ( t ) e − jω t d t また、関数f ( t ) f(t) f ( t ) F [ f ( t ) ] \mathcal{F}[f(t)] F [ f ( t )] F [ f ( t ) ] ( ω ) \mathcal{F}[f(t)](\omega) F [ f ( t )] ( ω ) F ( ω ) F(\omega) F ( ω )
ω \omega ω 2 π [ r a d ] 2 \pi \, [\mathit{\mathrm{rad}}] 2 π [ rad ] T = 2 π ω T=\frac{2 \pi}{\omega} T = ω 2 π f = 1 T = ω 2 π [ H z ] f = \frac{1}{T} = \frac{\omega}{2 \pi}\, [\mathrm{Hz}] f = T 1 = 2 π ω [ Hz ]
性質 数式 説明 線形性 F [ a f ( t ) + b g ( t ) ] = a F ( ω ) + b G ( ω ) \mathcal{F}[a f(t) + b g(t)] = a F(\omega) + b G(\omega) F [ a f ( t ) + b g ( t )] = a F ( ω ) + b G ( ω ) フーリエ変換は線形演算を保つ 時間シフト F [ f ( t − t 0 ) ] = e − j ω t 0 F ( ω ) \mathcal{F}[f(t - t_0)] = e^{-j\omega t_0} F(\omega) F [ f ( t − t 0 )] = e − jω t 0 F ( ω ) 関数の遅延は周波数領域で位相変化を引き起こす 周波数シフト F [ e j ω 0 t f ( t ) ] = F ( ω − ω 0 ) \mathcal{F}[e^{j \omega_0 t} f(t)] = F(\omega - \omega_0) F [ e j ω 0 t f ( t )] = F ( ω − ω 0 ) 時間領域での指数関数の乗算は周波数領域での平行移動に対応 時間スケーリング F [ f ( a t ) ] = 1 ∣ a ∣ F ( ω a ) \mathcal{F}[f(a t)] = \frac{1}{\lvert a \rvert} F ( \frac{\omega}{a} ) F [ f ( a t )] = ∣ a ∣ 1 F ( a ω ) 時間領域でのスケーリングは周波数領域で逆スケーリングと振幅の変化を引き起こす 時間反転 F [ f ( − t ) ] = F ( − ω ) \mathcal{F}[f(-t)] = F(-\omega) F [ f ( − t )] = F ( − ω ) 時間反転は周波数領域での反転に対応する 畳み込み F [ f ( t ) ∗ g ( t ) ] = F ( ω ) G ( ω ) \mathcal{F}[f(t) * g(t)] = F(\omega) G(\omega) F [ f ( t ) ∗ g ( t )] = F ( ω ) G ( ω ) 時間領域での畳み込みは周波数領域での積に対応する 時間領域での積 F [ f ( t ) g ( t ) ] = 1 2 π ( F ∗ G ) ( ω ) \mathcal{F}[f(t) g(t)] = \frac{1}{2\pi} (F * G)(\omega) F [ f ( t ) g ( t )] = 2 π 1 ( F ∗ G ) ( ω ) 時間領域での積は周波数領域での畳み込みに対応する 積分定理 F [ ∫ − ∞ t f ( τ ) d τ ] = 1 j ω F ( ω ) + π F ( 0 ) δ ( ω ) \mathcal{F} \left[ \int_{-\infty}^{t} f(\tau) d\tau \right] = \frac{1}{j\omega}F(\omega) + \pi F(0) \delta(\omega) F [ ∫ − ∞ t f ( τ ) d τ ] = jω 1 F ( ω ) + π F ( 0 ) δ ( ω ) 時間領域での積分は周波数領域での分数形式に変換される 微分定理 F [ f ′ ( t ) ] = j ω F ( ω ) \mathcal{F}[f'(t)] = j\omega F(\omega) F [ f ′ ( t )] = jω F ( ω ) 時間領域の微分は周波数領域での乗算に対応する フーリエ変換のフーリエ変換 F [ F [ f ( t ) ] ] = 2 π f ( − t ) \mathcal{F}[\mathcal{F}[f(t)]] = 2\pi f(-t) F [ F [ f ( t )]] = 2 π f ( − t ) 時間反転と振幅の変化を伴う
フーリエ級数
前述のフーリエ変換を得るために、本来はフーリエ級数→フーリエ積分→フーリエ変換と導出していくのが普通だが、本記事ではフーリエ変換は道具の1つなので、天下り的にフーリエ変換と級数を紹介する。フーリエ級数は、周期信号を三角関数の和に展開する。
区間− T 2 ≤ t ≤ T 2 -\frac{T}{2} \leq t \leq \frac{T}{2} − 2 T ≤ t ≤ 2 T f ( t ) f(t) f ( t ) T T T
f ( t ) = ∑ n = − ∞ ∞ C n e j n 2 π T t C n = 1 T ∫ − T 2 T 2 f ( t ) e − j n 2 π T t \begin{aligned}
f(t) &= \sum_{n=-\infty}^{\infty} C_n e^{jn\frac{2 \pi}{T}t} \\
C_n&=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) e^{-jn\frac{2 \pi}{T}t}
\end{aligned} f ( t ) C n = n = − ∞ ∑ ∞ C n e jn T 2 π t = T 1 ∫ − 2 T 2 T f ( t ) e − jn T 2 π t というフーリエ級数に展開できる。
離散フーリエ変換
前に示した動画のように、フーリエ変換のことを、ある信号を単位円上に巻きつけたその重心と考えるなら、離散的な信号を単位円上に巻きつけた時の重心は
∑ n = − ∞ ∞ f ( n T ) e − j ω n T \sum_{n=-\infty}^{\infty} f(nT)e^{-j \omega nT} n = − ∞ ∑ ∞ f ( n T ) e − jωn T と書ける。これが離散フーリエ変換の式である。
ラプラス変換
フーリエ変換には便利な性質がある。例えば、微分記号を外すことができる。
F [ f ( n ) ] ( ω ) = ( j ω ) n F [ f ] ( ω ) \mathcal{F}[f^{(n)}](\omega) = (j \omega)^{n} \mathcal{F}[f](\omega) F [ f ( n ) ] ( ω ) = ( jω ) n F [ f ] ( ω ) 現実世界の解析では微分方程式を解くことが多く、微分を外せるというフーリエ変換の性質は非常に便利である。
しかし、フーリエ変換の値が存在するためには、f ( t ) f(t) f ( t ) ( − ∞ , ∞ ) (- \infty, \infty) ( − ∞ , ∞ )
∫ − ∞ ∞ ∣ f ( t ) ∣ d t < ∞ \int_{-\infty}^{\infty} |f(t)| dt < \infty ∫ − ∞ ∞ ∣ f ( t ) ∣ d t < ∞ であることが必要である。これだとf ( t ) f(t) f ( t )
そこでf ( t ) f(t) f ( t ) t → ∞ t \rightarrow \infty t → ∞ t t t ( 0 , ∞ ) (0, \infty) ( 0 , ∞ ) σ ( σ > 0 ) \sigma \ (\sigma > 0) σ ( σ > 0 ) e − σ t f ( t ) e^{-\sigma t}f(t) e − σ t f ( t )
F [ e − σ t f ( t ) ] ( ω ) = ∫ 0 ∞ e − σ t f ( t ) e − j ω t d t = ∫ 0 ∞ f ( t ) e − ( σ + j ω ) t d t \begin{aligned}
\mathcal{F}[e^{-\sigma t}f(t)](\omega) &= \int_{0}^{\infty} e^{-\sigma t}f(t) e^{-j\omega t} dt \\
&= \int_{0}^{\infty} f(t) e^{- (\sigma + j\omega) t} dt
\end{aligned} F [ e − σ t f ( t )] ( ω ) = ∫ 0 ∞ e − σ t f ( t ) e − jω t d t = ∫ 0 ∞ f ( t ) e − ( σ + jω ) t d t ここで、σ + j ω \sigma + j\omega σ + jω s s s
L [ f ( t ) ] ( s ) = ∫ 0 ∞ f ( t ) e − s t d t \mathcal{L}[f(t)](s) = \int_{0}^{\infty} f(t) e^{- st} dt L [ f ( t )] ( s ) = ∫ 0 ∞ f ( t ) e − s t d t を得る。
関数f ( t ) f(t) f ( t ) L [ f ( t ) ] \mathcal{L}[f(t)] L [ f ( t )] L [ f ( t ) ] ( s ) \mathcal{L}[f(t)](s) L [ f ( t )] ( s ) F ( s ) F(s) F ( s )
s = j ω s=j \omega s = jω
L [ f ( t ) ] ( j ω ) = ∫ 0 ∞ f ( t ) e − j ω t d t \begin{aligned}
\mathcal{L}[f(t)](j \omega) = \int_{0}^{\infty} f(t) e^{- j \omega t} dt
\end{aligned} L [ f ( t )] ( jω ) = ∫ 0 ∞ f ( t ) e − jω t d t は、
F [ f ( t ) ] ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t \mathcal{F}[f(t)](\omega) = \int_{-\infty}^{\infty} f(t) e^{-j \omega t} dt F [ f ( t )] ( ω ) = ∫ − ∞ ∞ f ( t ) e − jω t d t と似ている。フーリエ変換がf ( t ) f(t) f ( t ) ( − ∞ , ∞ ) (-\infty, \infty) ( − ∞ , ∞ ) ( 0 , ∞ ) (0, \infty) ( 0 , ∞ )
性質 数式 説明 線形性 L [ a f ( t ) + b g ( t ) ] = a F ( s ) + b G ( s ) \mathcal{L}[a f(t) + b g(t)] = a F(s) + b G(s) L [ a f ( t ) + b g ( t )] = a F ( s ) + b G ( s ) ラプラス変換は線形演算を保つ 時間シフト L [ f ( t − t 0 ) u ( t − t 0 ) ] = e − s t 0 F ( s ) \mathcal{L}[f(t - t_0) u(t - t_0)] = e^{-st_0} F(s) L [ f ( t − t 0 ) u ( t − t 0 )] = e − s t 0 F ( s ) 関数の遅延が指数関数の乗算に変換 指数関数乗算の性質 L [ e s 0 t f ( t ) ] = F ( s − s 0 ) \mathcal{L}[e^{s_0t} f(t)] = F(s - s_0) L [ e s 0 t f ( t )] = F ( s − s 0 ) 時間領域での指数関数の乗算は変数の平行移動に対応 畳み込みのラプラス変換 L [ f ( t ) ∗ g ( t ) ] = F ( s ) G ( s ) \mathcal{L}[f(t) * g(t)]= F(s) G(s) L [ f ( t ) ∗ g ( t )] = F ( s ) G ( s ) 畳み込みはラプラス変換での積に対応 時間領域での積 L [ f ( t ) g ( t ) ] = 1 2 π j ∫ c − j ∞ c + j ∞ F ( σ ) G ( s − σ ) d σ \mathcal{L}[f(t) g(t)] = \frac{1}{2\pi j} \int_{c - j\infty}^{c + j\infty} F(\sigma) G(s - \sigma) d\sigma L [ f ( t ) g ( t )] = 2 πj 1 ∫ c − j ∞ c + j ∞ F ( σ ) G ( s − σ ) d σ 積はラプラス変換での複素畳み込みに対応 積分のラプラス変換 L [ ∫ 0 t f ( τ ) d τ ] = F ( s ) s \mathcal{L} [\int_0^t f(\tau) d\tau] = \frac{F(s)}{s} L [ ∫ 0 t f ( τ ) d τ ] = s F ( s ) 時間領域での積分はラプラス変換での除算に対応 微分のラプラス変換 L [ f ′ ( t ) ] = s F ( s ) − f ( 0 ) \mathcal{L} [f'(t)] = s F(s) - f(0) L [ f ′ ( t )] = s F ( s ) − f ( 0 ) 関数の微分がラプラス変換では乗算と初期値に対応 2階微分のラプラス変換 L [ f ′ ′ ( t ) ] = s 2 F ( s ) − s f ( 0 ) − f ′ ( 0 ) \mathcal{L}[f''(t)] = s^2 F(s) - s f(0) - f'(0) L [ f ′′ ( t )] = s 2 F ( s ) − s f ( 0 ) − f ′ ( 0 ) 高階微分も同様に変換できる
Z変換
離散版のラプラス変換のような物である。離散フーリエ変換の式に対して、ラプラス変換の導出と同じように求める。z z z
∑ n = 0 ∞ e − σ n T f ( n T ) e − j ω n T = ∑ k = 0 ∞ f ( n T ) e − ( σ + j ω ) n T = ∑ n = 0 ∞ f ( n T ) z − n \begin{aligned}
\sum_{n=0}^{\infty} e^{-\sigma nT}f(nT)e^{-j \omega nT} &= \sum_{k=0}^{\infty} f(nT)e^{- (\sigma + j \omega) nT} \\
&= \sum_{n=0}^{\infty} f(nT)z^{-n}
\end{aligned} n = 0 ∑ ∞ e − σn T f ( n T ) e − jωn T = k = 0 ∑ ∞ f ( n T ) e − ( σ + jω ) n T = n = 0 ∑ ∞ f ( n T ) z − n 関数f ( t ) f(t) f ( t ) Z [ f ( t ) ] \mathcal{Z}[f(t)] Z [ f ( t )] Z [ f ( t ) ] ( z ) \mathcal{Z}[f(t)](z) Z [ f ( t )] ( z ) F ( z ) F(z) F ( z )
z = e j ω T z=e^{j \omega T} z = e jω T
Z [ f ( t ) ] ( e j ω T ) = ∑ n = 0 ∞ f ( n T ) ( e j ω T ) − n = ∑ n = 0 ∞ f ( n T ) e − j ω n T \begin{aligned}
\mathcal{Z}[f(t)](e^{j \omega T}) &= \sum_{n=0}^{\infty} f(nT)(e^{j \omega T})^{-n} \\
&= \sum_{n=0}^{\infty} f(nT)e^{-j \omega nT}
\end{aligned} Z [ f ( t )] ( e jω T ) = n = 0 ∑ ∞ f ( n T ) ( e jω T ) − n = n = 0 ∑ ∞ f ( n T ) e − jωn T は、
F [ f ( n ) ] ( ω ) = ∑ n = − ∞ ∞ f ( n T ) e − j ω n T \mathcal{F}[f(n)](\omega) = \sum_{n=-\infty}^{\infty} f(nT)e^{-j \omega nT} F [ f ( n )] ( ω ) = n = − ∞ ∑ ∞ f ( n T ) e − jωn T と似ている。離散フーリエ変換がf ( t ) f(t) f ( t ) ( − ∞ , ∞ ) (-\infty, \infty) ( − ∞ , ∞ ) ( 0 , ∞ ) (0, \infty) ( 0 , ∞ )
性質 数式 説明 線形性 Z [ a f ( t ) + b g ( t ) ] = a F ( z ) + b G ( z ) \mathcal{Z}[a f(t) + b g(t)] = a F(z) + b G(z) Z [ a f ( t ) + b g ( t )] = a F ( z ) + b G ( z ) Z変換は線形演算を保つ 時間シフト Z [ f [ n − k ] ] = z − k F ( z ) \mathcal{Z}[f[n - k]] = z^{-k} F(z) Z [ f [ n − k ]] = z − k F ( z ) 時間領域のシフトは z z z 指数関数乗算の性質 Z [ α n f ( t ) ] = F ( z / α ) \mathcal{Z}[\alpha^n f(t)] = F(z/\alpha) Z [ α n f ( t )] = F ( z / α ) 時間領域での指数関数の乗算は変数のスケーリングに対応 畳み込みのZ変換 Z [ f ( t ) ∗ g ( t ) ] = F ( z ) G ( z ) \mathcal{Z}[f(t) * g(t)] = F(z) G(z) Z [ f ( t ) ∗ g ( t )] = F ( z ) G ( z ) 畳み込みはZ変換での積に対応 和のZ変換 Z [ ∑ k = 0 n f [ k ] ] = F ( z ) 1 − z − 1 \mathcal{Z} \left[ \sum_{k=0}^{n} f[k] \right] = \frac{F(z)}{1 - z^{-1}} Z [ ∑ k = 0 n f [ k ] ] = 1 − z − 1 F ( z ) 累積和はZ変換での除算に対応 微分のZ変換(離散時間) Z [ Δ f ( t ) ] = ( z − 1 ) F ( z ) \mathcal{Z} [\Delta f(t)] = (z - 1) F(z) Z [ Δ f ( t )] = ( z − 1 ) F ( z ) 離散差分はZ変換では乗算に対応 2階差分のZ変換 Z [ Δ 2 f ( t ) ] = ( z − 1 ) 2 F ( z ) \mathcal{Z} [\Delta^2 f(t)] = (z - 1)^2 F(z) Z [ Δ 2 f ( t )] = ( z − 1 ) 2 F ( z ) 高階差分も同様に変換できる
離散時間システムの表現
デジタルフィルタは離散時間システムである。離散時間システムへの入力信号と出力信号は整数n n n T T T f ( t ) f(t) f ( t ) f ( n T ) f(nT) f ( n T ) f [ n ] f[n] f [ n ]
離散時間信号とデジタル信号はほぼ同じ意味を持つが厳密には違う。離散時間信号の反対は連続時間信号であり、これは時間軸方向が離散であるかに着目した名前である。デジタル信号の反対はアナログ信号であり、これは時間軸方向と振幅方向が離散であるかに着目した名前である。
振幅方向が離散であるかどうかは、演算精度の議論でしか問題にならないため、本記事では離散時間信号とデジタル信号は同じ意味として使う。
離散時間信号を表現する重要なツールとして単位インパルス信号が挙げられる。
δ ( n T ) = { 1 , n = 0 0 , n ≠ 0 \delta (nT)=
\begin{cases}
1, & n=0 \\
0, & n \neq 0
\end{cases} δ ( n T ) = { 1 , 0 , n = 0 n = 0 これは次のような波形を持つ。
インパルス信号の頂点は並行移動することができ、整数k k k
δ ( n T − k T ) = { 1 , n = k 0 , n ≠ k \delta (nT-kT)=
\begin{cases}
1, & n=k \\
0, & n \neq k
\end{cases} δ ( n T − k T ) = { 1 , 0 , n = k n = k と書ける。これを用いれば任意の信号x ( n T ) x(nT) x ( n T )
x ( n T ) = ∑ k = − ∞ ∞ x ( k T ) δ ( n T − k T ) x(nT) = \sum_{k=-\infty}^{\infty} x(kT) \delta (nT - kT) x ( n T ) = k = − ∞ ∑ ∞ x ( k T ) δ ( n T − k T ) と書ける。これはかなり当たり前な式だが、離散時間システムを表現するうえで役立つ。
インパルス信号を用いて離散時間システムを表現することを考えよう。離散時間システムは、離散時間信号x ( n T ) x(nT) x ( n T ) y ( n T ) y(nT) y ( n T ) f f f
y ( n T ) = f [ x ( n T ) ] y(nT) = f[x(nT)] y ( n T ) = f [ x ( n T )] と書ける。図で表すなら下記の通りである。
システムにインパルス信号を入力したときの出力、インパルス応答をh ( n T ) = f [ δ ( n T ) ] h(nT)=f[\delta(nT)] h ( n T ) = f [ δ ( n T )]
前に述べたようにx ( n T ) = ∑ k = − ∞ ∞ x ( k T ) δ ( n T − k T ) x(nT) = \sum_{k=-\infty}^{\infty} x(kT) \delta (nT - kT) x ( n T ) = ∑ k = − ∞ ∞ x ( k T ) δ ( n T − k T )
y ( n T ) = f [ x ( n T ) ] = f [ ∑ k = − ∞ ∞ x ( k T ) δ ( n T − k T ) ] y(nT) = f[x(nT)] = f \left[ \sum_{k=-\infty}^{\infty} x(kT) \delta (nT - kT) \right] y ( n T ) = f [ x ( n T )] = f [ k = − ∞ ∑ ∞ x ( k T ) δ ( n T − k T ) ] と書ける。離散時間システムは線形性(EQ掛けてから信号を足しても、信号を足してからEQを掛けても結果は同じ)を持つから、
f [ a 1 x 1 ( n T ) + a 2 x 2 ( n T ) ] = a 1 f [ x 1 ( n T ) ] + a 2 f [ x 2 ( n T ) ] f[a_1x_1(nT)+a_2x_2(nT)] = a_1f[x_1(nT)]+a_2f[x_2(nT)] f [ a 1 x 1 ( n T ) + a 2 x 2 ( n T )] = a 1 f [ x 1 ( n T )] + a 2 f [ x 2 ( n T )] が成り立つので、
y ( n T ) = f [ x ( n T ) ] = f [ ∑ k = − ∞ ∞ x ( k T ) δ ( n T − k T ) ] = ∑ k = − ∞ ∞ f [ x ( k T ) δ ( n T − k T ) ] = ∑ k = − ∞ ∞ x ( k T ) f [ δ ( n T − k T ) ] \begin{aligned}
y(nT) = f[x(nT)] &= f \left[ \sum_{k=-\infty}^{\infty} x(kT) \delta (nT - kT) \right] \\
&= \sum_{k=-\infty}^{\infty} f \left[x(kT) \delta (nT - kT) \right] \\
&= \sum_{k=-\infty}^{\infty} x(kT) f \left[ \delta (nT - kT) \right]
\end{aligned} y ( n T ) = f [ x ( n T )] = f [ k = − ∞ ∑ ∞ x ( k T ) δ ( n T − k T ) ] = k = − ∞ ∑ ∞ f [ x ( k T ) δ ( n T − k T ) ] = k = − ∞ ∑ ∞ x ( k T ) f [ δ ( n T − k T ) ] ここで、離散時間システムは時不変性(いつ入力しても結果は同じ)を持つので、インパルス応答の式からh ( n T − k T ) = f [ δ ( n T − k T ) ] h(nT-kT)=f[\delta(nT-kT)] h ( n T − k T ) = f [ δ ( n T − k T )]
y ( n T ) = f [ x ( n T ) ] = ∑ k = − ∞ ∞ x ( k T ) f [ δ ( n T − k T ) ] = ∑ k = − ∞ ∞ x ( k T ) h ( n T − k T ) \begin{aligned}
y(nT) = f[x(nT)] &= \sum_{k=-\infty}^{\infty} x(kT) f \left[ \delta (nT - kT) \right] \\
&= \sum_{k=-\infty}^{\infty} x(kT) h(nT-kT)
\end{aligned} y ( n T ) = f [ x ( n T )] = k = − ∞ ∑ ∞ x ( k T ) f [ δ ( n T − k T ) ] = k = − ∞ ∑ ∞ x ( k T ) h ( n T − k T ) この式の右辺の形を畳み込み和(コンボリューション)と呼ぶ。つまり、任意の入力信号に対する出力信号は、システムのインパルス応答を入力信号に畳み込むと得られるということが分かる。
また、当たり前な式だと紹介したx ( n T ) = ∑ k = − ∞ ∞ x ( k T ) δ ( n T − k T ) x(nT) = \sum_{k=-\infty}^{\infty} x(kT) \delta (nT - kT) x ( n T ) = ∑ k = − ∞ ∞ x ( k T ) δ ( n T − k T ) δ ( n T ) \delta(nT) δ ( n T )
システムのインパルス応答が有限長であればそのシステムはFIRシステム(Finite Impulse Response)であり、無限長であればIIRシステム(Infinite Impulse Response)である。
現実のシステムを考える際、FIRシステムであれば有限長のインパルス応答を畳み込めば良いので実現可能である。ただし、無限長のインパルス応答を畳み込むのは不可能であるためIIRシステムは実現できないように見える。しかし、差分方程式を使うことでIIRシステムは上手いこと実現可能である。
具体的に見てみる。インパルス応答が下記式で表せるようなIIRシステムを考える。
h ( n T ) = { α n , 0 ≤ n 0 , otherwise h(nT) =
\begin{cases}
\alpha ^n, & 0 \leq n \\
0, & \text{otherwise}
\end{cases} h ( n T ) = { α n , 0 , 0 ≤ n otherwise インパルス応答h ( n T ) h(nT) h ( n T ) n < 0 n<0 n < 0 h ( n T ) h(nT) h ( n T ) n < 0 n<0 n < 0 h ( n T ) h(nT) h ( n T ) n < 0 n<0 n < 0 x ( n T ) x(nT) x ( n T ) y ( n T ) y(nT) y ( n T )
y ( n T ) = f [ x ( n T ) ] = ∑ k = − ∞ ∞ x ( k T ) h ( n T − k T ) = ∑ k = − ∞ ∞ h ( k T ) x ( n T − k T ) ※畳み込みは可換 = ∑ k = 0 ∞ α k x ( n T − k T ) \begin{aligned}
y(nT) = f[x(nT)] &= \sum_{k=-\infty}^{\infty} x(kT) h(nT-kT) \\
&= \sum_{k=-\infty}^{\infty} h(kT) x(nT-kT) \quad \scriptsize{※畳み込みは可換}\\
&= \sum_{k=0}^{\infty} \alpha^k x(nT-kT)
\end{aligned} y ( n T ) = f [ x ( n T )] = k = − ∞ ∑ ∞ x ( k T ) h ( n T − k T ) = k = − ∞ ∑ ∞ h ( k T ) x ( n T − k T ) ※ 畳み込みは可換 = k = 0 ∑ ∞ α k x ( n T − k T ) 具体的なn n n k k k
y ( 0 × T ) = ∑ k = 0 ∞ α k x ( − k T ) = α 0 x ( 0 ) + α 1 x ( − T ) + α 2 x ( − 2 T ) + α 3 x ( − 3 T ) + α 4 x ( − 4 T ) + ⋯ y ( 1 × T ) = ∑ k = 0 ∞ α k x ( T − k T ) = α 0 x ( T ) + α 1 x ( 0 ) + α 2 x ( − T ) + α 3 x ( − 2 T ) + α 4 x ( − 3 T ) + ⋯ = α 0 x ( T ) + α ( α 0 x ( 0 ) + α 1 x ( − T ) + α 2 x ( − 2 T ) + α 3 x ( − 3 T ) + ⋯ ) = α 0 x ( T ) + α y ( 0 × T ) y ( 2 × T ) = ∑ k = 0 ∞ α k x ( 2 T − k T ) = α 0 x ( 2 T ) + α 1 x ( T ) + α 2 x ( 0 ) + α 3 x ( − T ) + α 4 x ( − 2 T ) + ⋯ = α 0 x ( 2 T ) + α ( α 0 x ( T ) + α 1 x ( 0 ) + α 2 x ( − T ) + α 3 x ( − 2 T ) + ⋯ ) = α 0 x ( 2 T ) + α y ( 1 × T ) \begin{aligned}
y(0 \times T) &= \sum_{k=0}^{\infty} \alpha^k x(-kT) \\
&= \alpha^0 x(0) + \alpha^1 x(-T) + \alpha^2 x(-2T) + \alpha^3 x(-3T) + \alpha^4 x(-4T) + \cdots \\
y(1 \times T) &= \sum_{k=0}^{\infty} \alpha^k x(T-kT) \\
&= \alpha^0 x(T) + \alpha^1 x(0) + \alpha^2 x(-T) + \alpha^3 x(-2T) + \alpha^4 x(-3T) + \cdots \\
&= \alpha^0 x(T) + \alpha ( \alpha^0 x(0) + \alpha^1 x(-T) + \alpha^2 x(-2T) + \alpha^3 x(-3T) + \cdots )\\
&= \alpha^0 x(T) + \alpha y(0 \times T) \\
y(2 \times T) &= \sum_{k=0}^{\infty} \alpha^k x(2T-kT) \\
&= \alpha^0 x(2T) + \alpha^1 x(T) + \alpha^2 x(0) + \alpha^3 x(-T) + \alpha^4 x(-2T) + \cdots \\
&= \alpha^0 x(2T) + \alpha (\alpha^0 x(T) + \alpha^1 x(0) + \alpha^2 x(-T) + \alpha^3 x(-2T) + \cdots ) \\
&= \alpha^0 x(2T) + \alpha y (1 \times T)
\end{aligned} y ( 0 × T ) y ( 1 × T ) y ( 2 × T ) = k = 0 ∑ ∞ α k x ( − k T ) = α 0 x ( 0 ) + α 1 x ( − T ) + α 2 x ( − 2 T ) + α 3 x ( − 3 T ) + α 4 x ( − 4 T ) + ⋯ = k = 0 ∑ ∞ α k x ( T − k T ) = α 0 x ( T ) + α 1 x ( 0 ) + α 2 x ( − T ) + α 3 x ( − 2 T ) + α 4 x ( − 3 T ) + ⋯ = α 0 x ( T ) + α ( α 0 x ( 0 ) + α 1 x ( − T ) + α 2 x ( − 2 T ) + α 3 x ( − 3 T ) + ⋯ ) = α 0 x ( T ) + α y ( 0 × T ) = k = 0 ∑ ∞ α k x ( 2 T − k T ) = α 0 x ( 2 T ) + α 1 x ( T ) + α 2 x ( 0 ) + α 3 x ( − T ) + α 4 x ( − 2 T ) + ⋯ = α 0 x ( 2 T ) + α ( α 0 x ( T ) + α 1 x ( 0 ) + α 2 x ( − T ) + α 3 x ( − 2 T ) + ⋯ ) = α 0 x ( 2 T ) + α y ( 1 × T ) 段々法則も分かって来たので、
y ( n T ) = f [ x ( n T ) ] = ∑ k = 0 ∞ α k x ( n T − k T ) = x ( n T ) + ∑ k = 1 ∞ α k x ( n T − k T ) = x ( n T ) + ∑ k = 0 ∞ α k + 1 x ( n T − ( k + 1 ) T ) = x ( n T ) + α ∑ k = 0 ∞ α k x ( ( n − 1 ) T − k T ) = x ( n T ) + α y ( ( n − 1 ) T ) \begin{aligned}
y(nT) = f[x(nT)] &= \sum_{k=0}^{\infty} \alpha^k x(nT-kT) \\
&= x(nT) + \sum_{k=1}^{\infty} \alpha^{k} x(nT-kT) \\
&= x(nT) + \sum_{k=0}^{\infty} \alpha^{k+1} x(nT-(k+1)T) \\
&= x(nT) + \alpha \sum_{k=0}^{\infty} \alpha^{k} x((n-1)T-kT) \\
&= x(nT) + \alpha y((n-1)T)
\end{aligned} y ( n T ) = f [ x ( n T )] = k = 0 ∑ ∞ α k x ( n T − k T ) = x ( n T ) + k = 1 ∑ ∞ α k x ( n T − k T ) = x ( n T ) + k = 0 ∑ ∞ α k + 1 x ( n T − ( k + 1 ) T ) = x ( n T ) + α k = 0 ∑ ∞ α k x (( n − 1 ) T − k T ) = x ( n T ) + α y (( n − 1 ) T ) 以上より、前の結果を定数倍して現在の信号に加算すれば実現可能ということが分かった。
これを一般化すれば、離散時間システムの入出力関係の式は
y ( n T ) = a 0 x ( n T ) + a 1 x ( n T − T ) + ⋯ + a M x ( n T − M T ) − ( b 0 y ( n T ) + b 1 y ( n T − T ) + ⋯ + b M y ( n T − N T ) ) = ∑ k = 0 M a k x ( n T − k T ) − ∑ k = 1 N b k y ( n T − k T ) \begin{aligned}
y(nT) &= a_0x(nT) + a_1x(nT-T) + \cdots + a_Mx(nT-MT) \\
& \qquad -(b_0y(nT) + b_1y(nT-T) + \cdots + b_My(nT-NT)) \\
&= \sum_{k=0}^{M} a_k x(nT-kT) - \sum_{k=1}^{N}b_ky(nT-kT) \\
\end{aligned} y ( n T ) = a 0 x ( n T ) + a 1 x ( n T − T ) + ⋯ + a M x ( n T − MT ) − ( b 0 y ( n T ) + b 1 y ( n T − T ) + ⋯ + b M y ( n T − NT )) = k = 0 ∑ M a k x ( n T − k T ) − k = 1 ∑ N b k y ( n T − k T ) となる。これを差分方程式と呼ぶ。M M M N N N
離散時間システムの解析
離散時間システムの解析にはZ変換を用いる。これは離散時間におけるラプラス変換のような物である。電気回路などの連続時間システムの解析にラプラス変換を用いることと対応づけると良い。
直前の項で、離散時間システムの入出力関係は差分方程式で表せると述べた。この差分方程式の両辺をZ変換してみる。
Y ( z ) = ∑ k = 0 M a k z − k X ( Z ) − ∑ k = 1 N b k z − k Y ( z ) Y ( z ) X ( z ) = ∑ k = 0 M a k z − k 1 + ∑ k = 1 N b k z − k \begin{aligned}
Y(z) &= \sum_{k=0}^{M} a_k z^{-k} X(Z) - \sum_{k=1}^{N} b_k z^{-k}Y(z) \\
\frac{Y(z)}{X(z)} &= \frac{\sum_{k=0}^{M} a_k z^{-k}}{1+\sum_{k=1}^{N} b_k z^{-k}}
\end{aligned} Y ( z ) X ( z ) Y ( z ) = k = 0 ∑ M a k z − k X ( Z ) − k = 1 ∑ N b k z − k Y ( z ) = 1 + ∑ k = 1 N b k z − k ∑ k = 0 M a k z − k 入出力の信号のZ変換の関係式Y ( z ) X ( z ) \frac{Y(z)}{X(z)} X ( z ) Y ( z ) H ( z ) H(z) H ( z ) z = e j ω T z=e^{j\omega T} z = e jω T z = e j ω T z=e^{j\omega T} z = e jω T H ( ω ) H(\omega) H ( ω )
周波数特性H ( ω ) H(\omega) H ( ω ) ∣ H ( ω ) ∣ |H(\omega)| ∣ H ( ω ) ∣ arg ( H ( ω ) ) \arg(H(\omega)) arg ( H ( ω ))
プラグインでよく見るスペクトラムアナライザは振幅特性の2乗に対数をとったもの、つまり、
log 10 ( ∣ H ( ω ) ∣ 2 ) = 2 log 10 ( ∣ H ( ω ) ∣ ) [ B ] ※単位はベル = 20 log 10 ( ∣ H ( ω ) ∣ ) [ d B ] ※単位はデシベル \begin{aligned}
\log_{10}(|H(\omega)|^2) &= 2 \log_{10}(|H(\omega)|)\ [\mathrm{B}] \quad \footnotesize{※単位はベル} \\
&= 20 \log_{10}(|H(\omega)|)\ [\mathrm{dB}] \quad \footnotesize{※単位はデシベル}
\end{aligned} log 10 ( ∣ H ( ω ) ∣ 2 ) = 2 log 10 ( ∣ H ( ω ) ∣ ) [ B ] ※ 単位はベル = 20 log 10 ( ∣ H ( ω ) ∣ ) [ dB ] ※ 単位はデシベル の式で得られたものの内、正の周波数を表示したものである。
標本化定理(サンプリング定理)
アナログ世界の信号は連続信号であることが多い。これをデジタル世界で処理する為には、連続信号を離散信号に変換する必要がある。時間方向に離散化することを「標本化」や「サンプリング」と呼ぶ。振幅方向に離散化することを「量子化」と呼ぶ。
連続信号f ( t ) f(t) f ( t ) T T T f ( t ) f(t) f ( t ) T T T
f s a m p l e d ( t ) = { f ( n T ) , t = n T ( n は整数 ) 0 , otherwise f_{\mathit{sampled}}(t) =
\begin{cases}
f(nT), & t = nT\quad (n は整数) \\
0, & \text{otherwise}
\end{cases} f sampled ( t ) = { f ( n T ) , 0 , t = n T ( n は整数 ) otherwise と書けるため、フーリエ変換の式は下記のようになりそう。
F = ∫ − ∞ ∞ f s a m p l e d ( t ) e − i ω t d t \mathcal{F}=\int_{-\infty}^{\infty} f_{\mathit{sampled}}(t) e^{-i\omega t} dt F = ∫ − ∞ ∞ f sampled ( t ) e − iω t d t しかし、f s a m p l e d ( t ) f_{\mathit{sampled}}(t) f sampled ( t ) f s a m p l e d ( t ) f_{\mathit{sampled}}(t) f sampled ( t )
そこでディラックのデルタ関数を用意する。この関数は任意の連続な関数g ( x ) g(x) g ( x )
∫ − ∞ ∞ g ( x ) δ ( x ) d x = g ( 0 ) \int_{-\infty}^{\infty} g(x) \delta(x) \, dx = g(0) ∫ − ∞ ∞ g ( x ) δ ( x ) d x = g ( 0 ) ディラックのデルタ関数は「関数(function)」という名前がついているが正しくは「超関数(distribution)」であり、関数ではない。なのでδ ( x ) = 〇〇 \delta(x)=〇〇 δ ( x ) = 〇〇 g ( x ) = 1 g(x)=1 g ( x ) = 1
∫ − ∞ ∞ δ ( x ) d x = 1 \int_{-\infty}^{\infty} \delta(x) \, dx = 1 ∫ − ∞ ∞ δ ( x ) d x = 1 を得る。つまり、ディラックのデルタ関数の面積は1である。また定義式から、g ( x ) δ ( x ) g(x) \delta(x) g ( x ) δ ( x ) x = 0 x=0 x = 0 g ( 0 ) g(0) g ( 0 ) x = 0 x=0 x = 0
δ ( x ) = { ∞ , x = 0 0 , x ≠ 0 \delta(x) =
\begin{cases}
\infty, & x = 0 \\
0, & x \neq 0
\end{cases} δ ( x ) = { ∞ , 0 , x = 0 x = 0 のようなイメージができる。なぜ1 1 1 ∞ \infty ∞ ∞ \infty ∞
注意しなければならないのが、これはあくまでもイメージということである。信号処理の分野では、δ ( 0 ) \delta (0) δ ( 0 ) 1 1 1
このディラックのデルタ関数を間隔T T T
δ T ( t ) = ∑ n = − ∞ ∞ δ ( t − n T ) \delta_T(t) = \sum_{n=-\infty}^{\infty} \delta(t-nT) δ T ( t ) = n = − ∞ ∑ ∞ δ ( t − n T ) と書ける。デルタ関数列と連続信号f ( t ) f(t) f ( t ) f s a m p l e d ( t ) f_{\mathit{sampled}}(t) f sampled ( t )
f s a m p l e d ( t ) = f ( t ) δ T ( t ) f_{\mathit{sampled}}(t)=f(t)\delta_T(t) f sampled ( t ) = f ( t ) δ T ( t ) ディラックのデルタ関数の性質を考えると、f s a m p l e d ( t ) = f ( t ) δ T ( t ) f_{\mathit{sampled}}(t)=f(t)\delta_T(t) f sampled ( t ) = f ( t ) δ T ( t ) ∞ \infty ∞
δ ( x ) = { ∞ , x = 0 0 , x ≠ 0 \delta(x) =
\begin{cases}
\infty, & x = 0 \\
0, & x \neq 0
\end{cases} δ ( x ) = { ∞ , 0 , x = 0 x = 0 ただ、上述の性質はあくまでもイメージであることと、この後f s a m p l e d ( t ) f_{\mathit{sampled}}(t) f sampled ( t )
ちなみに。ディラックのデルタ関数と一般の関数f ( t ) f(t) f ( t )
∫ − ∞ ∞ f ( u ) δ ( t − u ) d u = ∫ − ∞ ∞ δ ( u ) f ( t − u ) d u = f ( t ) \begin{aligned}
\int_{-\infty}^{\infty} f(u)\delta (t-u) \, du &= \int_{-\infty}^{\infty} \delta(u) f(t-u) \, du = f(t)
\end{aligned} ∫ − ∞ ∞ f ( u ) δ ( t − u ) d u = ∫ − ∞ ∞ δ ( u ) f ( t − u ) d u = f ( t ) これをディラックのデルタ関数の定義としても良い。この式から、ディラックのデルタ関数は畳み込み演算に置ける単位元と言える。離散時間システムの表現の項で、離散時間畳み込み和の単位元はインパルス信号であると書いた。連続時間信号畳み込みの単位元がディラックのデルタ関数である事実と照らし合わせると良い。
いよいよf s a m p l e d ( t ) = f ( t ) δ T ( t ) f_{\mathit{sampled}}(t)=f(t)\delta_T(t) f sampled ( t ) = f ( t ) δ T ( t )
F [ f ( t ) δ T ( t ) ] ( ω ) = 1 2 π ∫ − ∞ ∞ F [ f ( t ) ] ( u ) ⋅ F [ δ T ( t ) ] ( ω − u ) d u \begin{aligned}
\mathcal{F}[f(t)\delta_T(t)](\omega) = \frac{1}{2 \pi} \int_{-\infty}^{\infty} \mathcal{F}[f(t)](u) \cdot \mathcal{F}[\delta_T(t)](\omega - u) \, du
\end{aligned} F [ f ( t ) δ T ( t )] ( ω ) = 2 π 1 ∫ − ∞ ∞ F [ f ( t )] ( u ) ⋅ F [ δ T ( t )] ( ω − u ) d u を計算すれば良い。まず、デルタ関数列のフーリエ変換から行う。
デルタ関数列は周期T T T
δ T ( t ) = ∑ n = − ∞ ∞ ( 1 T ∫ − T 2 T 2 δ ( t ) e − j n 2 π T t ) e j n 2 π T t = 1 T ∑ n = − ∞ ∞ e j n 2 π T t \begin{aligned}
\delta_T(t) &= \sum_{n=-\infty}^{\infty} \left( \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} \delta(t) e^{-jn\frac{2 \pi}{T}t} \right) e^{jn\frac{2 \pi}{T}t} \\
&= \frac{1}{T} \sum_{n=-\infty}^{\infty} e^{jn\frac{2 \pi}{T}t}
\end{aligned} δ T ( t ) = n = − ∞ ∑ ∞ ( T 1 ∫ − 2 T 2 T δ ( t ) e − jn T 2 π t ) e jn T 2 π t = T 1 n = − ∞ ∑ ∞ e jn T 2 π t これをフーリエ変換すると
F [ δ T ( t ) ] ( ω ) = ∫ − ∞ ∞ δ T ( t ) e − j ω t d t = ∫ − ∞ ∞ ( 1 T ∑ n = − ∞ ∞ e j n 2 π T t ) e − j ω t d t = 1 T ∑ n = − ∞ ∞ ∫ − ∞ ∞ e j n 2 π T t e − j ω t d t \begin{aligned}
\mathcal{F}[\delta_T(t)](\omega) &= \int_{-\infty}^{\infty} \delta_T(t) e^{-j \omega t} \, dt \\
&= \int_{-\infty}^{\infty} \left( \frac{1}{T} \sum_{n=-\infty}^{\infty} e^{jn\frac{2 \pi}{T}t} \right) e^{-j \omega t} \, dt \\
&= \frac{1}{T} \sum_{n=-\infty}^{\infty} \int_{-\infty}^{\infty} e^{jn\frac{2 \pi}{T}t} e^{-j \omega t} \, dt \\
\end{aligned} F [ δ T ( t )] ( ω ) = ∫ − ∞ ∞ δ T ( t ) e − jω t d t = ∫ − ∞ ∞ ( T 1 n = − ∞ ∑ ∞ e jn T 2 π t ) e − jω t d t = T 1 n = − ∞ ∑ ∞ ∫ − ∞ ∞ e jn T 2 π t e − jω t d t ここで、ディラックのデルタ関数のフーリエ変換F [ δ ( t ) ] ( ω ) = 1 \mathcal{F}[\delta(t)](\omega)=1 F [ δ ( t )] ( ω ) = 1 F [ 1 ] ( ω ) = 2 π δ ( ω ) \mathcal{F}[1](\omega)=2 \pi \delta(\omega) F [ 1 ] ( ω ) = 2 π δ ( ω ) F [ 1 ⋅ e j ω 0 t ] ( ω ) = 2 π δ ( ω − ω 0 ) \mathcal{F}[1 \cdot e^{j \omega_0 t}](\omega)=2 \pi \delta(\omega - \omega_0) F [ 1 ⋅ e j ω 0 t ] ( ω ) = 2 π δ ( ω − ω 0 )
F [ δ T ( t ) ] ( ω ) = ∫ − ∞ ∞ δ T ( t ) e − j ω t d t = 1 T ∑ n = − ∞ ∞ 2 π δ ( ω − n 2 π T ) = 2 π T ∑ n = − ∞ ∞ δ ( ω − n 2 π T ) \begin{aligned}
\mathcal{F}[\delta_T(t)](\omega) &= \int_{-\infty}^{\infty} \delta_T(t) e^{-j \omega t} \, dt \\
&= \frac{1}{T} \sum_{n=-\infty}^{\infty} 2 \pi \delta(\omega - n\frac{2 \pi}{T}) \\
&= \frac{2 \pi}{T} \sum_{n=-\infty}^{\infty} \delta(\omega - n\frac{2 \pi}{T}) \\
\end{aligned} F [ δ T ( t )] ( ω ) = ∫ − ∞ ∞ δ T ( t ) e − jω t d t = T 1 n = − ∞ ∑ ∞ 2 π δ ( ω − n T 2 π ) = T 2 π n = − ∞ ∑ ∞ δ ( ω − n T 2 π ) これを使えばf s a m p l e d ( t ) = f ( t ) δ T ( t ) f_{\mathit{sampled}}(t)=f(t)\delta_T(t) f sampled ( t ) = f ( t ) δ T ( t )
F [ f ( t ) δ T ( t ) ] ( ω ) = 1 2 π ∫ − ∞ ∞ F [ f ( t ) ] ( u ) ⋅ F [ δ T ( t ) ] ( ω − u ) d u = 1 2 π ∫ − ∞ ∞ F [ f ( t ) ] ( u ) ⋅ 2 π T ∑ n = − ∞ ∞ δ ( ω − n 2 π T − u ) d u = 1 T ∑ n = − ∞ ∞ ∫ − ∞ ∞ F [ f ( t ) ] ( u ) ⋅ δ ( ω − n 2 π T − u ) d u \begin{aligned}
\mathcal{F}[f(t)\delta_T(t)](\omega) &= \frac{1}{2 \pi} \int_{-\infty}^{\infty} \mathcal{F}[f(t)](u) \cdot \mathcal{F}[\delta_T(t)](\omega - u) \, du \\
&= \frac{1}{2 \pi} \int_{-\infty}^{\infty} \mathcal{F}[f(t)](u) \cdot \frac{2 \pi}{T} \sum_{n=-\infty}^{\infty} \delta(\omega - n\frac{2 \pi}{T} - u) \, du \\
&= \frac{1}{T} \sum_{n=-\infty}^{\infty} \int_{-\infty}^{\infty} \mathcal{F}[f(t)](u) \cdot \delta(\omega - n\frac{2 \pi}{T} - u) \, du \\
\end{aligned} F [ f ( t ) δ T ( t )] ( ω ) = 2 π 1 ∫ − ∞ ∞ F [ f ( t )] ( u ) ⋅ F [ δ T ( t )] ( ω − u ) d u = 2 π 1 ∫ − ∞ ∞ F [ f ( t )] ( u ) ⋅ T 2 π n = − ∞ ∑ ∞ δ ( ω − n T 2 π − u ) d u = T 1 n = − ∞ ∑ ∞ ∫ − ∞ ∞ F [ f ( t )] ( u ) ⋅ δ ( ω − n T 2 π − u ) d u ディラックのデルタ関数は畳み込み演算に置ける単位元なので、
F [ f ( t ) δ T ( t ) ] ( ω ) = 1 T ∑ n = − ∞ ∞ ∫ − ∞ ∞ F [ f ( t ) ] ( u ) ⋅ δ ( ω − n 2 π T − u ) d u = 1 T ∑ n = − ∞ ∞ F [ f ( t ) ] ( ω − n 2 π T ) = 1 T ∑ n = − ∞ ∞ F ( ω − n 2 π T ) \begin{aligned}
\mathcal{F}[f(t)\delta_T(t)](\omega) &= \frac{1}{T} \sum_{n=-\infty}^{\infty} \int_{-\infty}^{\infty} \mathcal{F}[f(t)](u) \cdot \delta(\omega - n\frac{2 \pi}{T} - u) \, du \\
&= \frac{1}{T} \sum_{n=-\infty}^{\infty} \mathcal{F}[f(t)](\omega - n\frac{2 \pi}{T}) \\
&= \frac{1}{T} \sum_{n=-\infty}^{\infty} F(\omega - n\frac{2 \pi}{T})
\end{aligned} F [ f ( t ) δ T ( t )] ( ω ) = T 1 n = − ∞ ∑ ∞ ∫ − ∞ ∞ F [ f ( t )] ( u ) ⋅ δ ( ω − n T 2 π − u ) d u = T 1 n = − ∞ ∑ ∞ F [ f ( t )] ( ω − n T 2 π ) = T 1 n = − ∞ ∑ ∞ F ( ω − n T 2 π ) この式を解釈すると、連続時間信号をサンプリングした離散信号のスペクトルは、連続時間信号のスペクトルを間隔2 π T \frac{2 \pi}{T} T 2 π 2 π T \frac{2 \pi}{T} T 2 π
連続時間信号のスペクトルの最大値がσ \sigma σ σ \sigma σ σ ≥ 1 2 × 2 π T \sigma \geq \frac{1}{2} \times \frac{2 \pi}{T} σ ≥ 2 1 × T 2 π
折角なのでサンプリングした信号から連続時間信号を復元する処理も行ってみよう。ここではエイリアシング歪みが無かった時を考える。
連続時間信号をサンプリングした離散信号のスペクトルは、連続時間信号のスペクトルを間隔2 π T \frac{2 \pi}{T} T 2 π
カットオフ周波数がω c \omega_c ω c
H ( ω ) = { 1 , ∣ ω ∣ ≤ ω C 0 , ω C < ∣ ω ∣ H(\omega) =
\begin{cases}
1, & |\omega| \leq \omega_C \\
0, & \omega_C < |\omega|
\end{cases} H ( ω ) = { 1 , 0 , ∣ ω ∣ ≤ ω C ω C < ∣ ω ∣ 理想低域通過フィルタを時間領域で表現するにはH ( ω ) H(\omega) H ( ω )
h ( t ) = 1 2 π ∫ − ω c ω c e j ω t = ω c π sin ω c t ω c t h(t) = \frac{1}{2 \pi} \int_{-\omega_c}^{\omega_c} e^{j \omega t} = \frac{\omega_c}{\pi} \frac{\sin \omega_ct}{\omega_ct} h ( t ) = 2 π 1 ∫ − ω c ω c e jω t = π ω c ω c t sin ω c t である。これはsinc関数である。
周波数領域にて、サンプリングした離散信号のスペクトルにH ( ω ) H(\omega) H ( ω )
今回はサンプリング定理の説明を数式で行ったが、もっと直感的な説明も可能である。
例えば下図左側は周波数が0.25Hzの連続信号を1Hzでサンプリングした様子を示している。赤い点だけみても、波の形を保てているのが分かる。下図中央は周波数が0.33Hzの連続信号を1Hzでサンプリングしている。こちらも波の形を保てている。しかし、下図右側のように周波数が0.5Hzの連続信号、つまりナイキスト周波数と丁度同じ周波数を持つ信号を1Hzでサンプリングすると、波の形を保てていないことが分かる。
Chapter 2. IIRデジタルフィルタの設計
いよいよIIRデジタルフィルタの設計に移る。実は、IIRデジタルフィルタを無から作り出すのは難しい。そこで、アナログフィルタの理論は昔からよく研究されていることから、アナログフィルタを何等かの形で変換してデジタルフィルタを得ることを考えよう。ここではいくつかの方法を紹介する。
電気回路からの直接設計
下記はRCローパスフィルタの回路である。これをデジタルフィルタとして設計し、プログラムで実装可能なブロックダイアグラムを得ることを目的とする。
周波数特性の確認
まずはこの回路がどのような周波数特性を持つのかを確認する。
この回路について成り立つ式は次の通り。
V x = V r + V c V y = V c V r = I R I = d Q c d t Q c = C V c \begin{aligned}
V_x &= V_r + V_c \\
V_y &= V_c \\
V_r &= IR \\
I &= \frac{d Q_c}{dt} \\
Q_c &= C V_c
\end{aligned} V x V y V r I Q c = V r + V c = V c = I R = d t d Q c = C V c これを整理すると次のようになる。
V x = V r + V c = I R + V y = R d Q c d t + V y = R d C V c d t + V y = R d C V y d t + V y = R C d V y d t + V y \begin{aligned}
V_x &= V_r + V_c \\
&= IR + V_y \\
&= R \frac{d Q_c}{dt} + V_y \\
&= R \frac{d C V_c}{dt} + V_y \\
&= R \frac{d C V_y}{dt} + V_y \\
&= R C \frac{d V_y}{dt} + V_y
\end{aligned} V x = V r + V c = I R + V y = R d t d Q c + V y = R d t d C V c + V y = R d t d C V y + V y = RC d t d V y + V y 微分方程式となり少々厄介なので、両辺をラプラス変換して微分を消す。
L [ V x ] ( s ) = s R C L [ V y ] ( s ) + L [ V y ] ( s ) = ( 1 + s R C ) L [ V y ] ( s ) \begin{aligned}
\mathcal{L}[V_x](s) &= s R C \mathcal{L}[V_y](s) + \mathcal{L}[V_y](s) \\
&= (1+sRC) \mathcal{L}[V_y](s)
\end{aligned} L [ V x ] ( s ) = s RC L [ V y ] ( s ) + L [ V y ] ( s ) = ( 1 + s RC ) L [ V y ] ( s ) この回路の周波数特性を知るためには、入出力信号の周波数特性の比F [ V y ] ( ω ) F [ V x ] ( ω ) \frac{\mathcal{F}[V_y](\omega)}{\mathcal{F}[V_x](\omega)} F [ V x ] ( ω ) F [ V y ] ( ω ) F [ V y ] ( ω ) = L [ V y ] ( j ω ) \mathcal{F}[V_y](\omega)=\mathcal{L}[V_y](j \omega) F [ V y ] ( ω ) = L [ V y ] ( jω ) F [ V x ] ( ω ) = L [ V x ] ( j ω ) \mathcal{F}[V_x](\omega)=\mathcal{L}[V_x](j \omega) F [ V x ] ( ω ) = L [ V x ] ( jω ) H ( s ) H(s) H ( s )
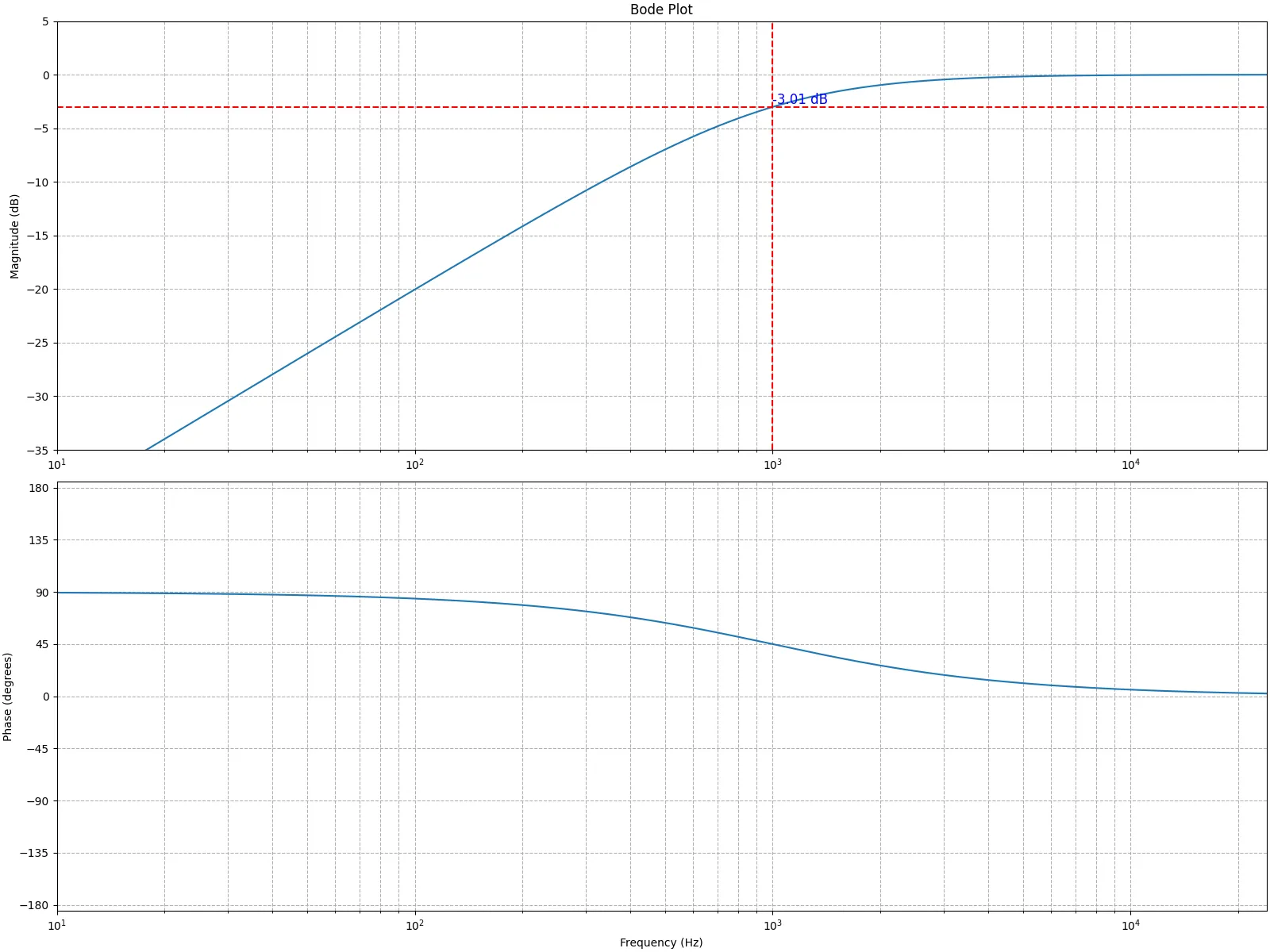
H ( s ) = L [ V y ] ( s ) L [ V x ] ( s ) = 1 1 + s R C H(s) = \frac{\mathcal{L}[V_y](s)}{\mathcal{L}[V_x](s)} = \frac{1}{1+sRC} H ( s ) = L [ V x ] ( s ) L [ V y ] ( s ) = 1 + s RC 1 となり、周波数特性H ( j ω ) H(j \omega) H ( jω )
H ( j ω ) = L [ V y ] ( j ω ) L [ V x ] ( j ω ) = 1 1 + j ω R C H(j \omega) = \frac{\mathcal{L}[V_y](j \omega)}{\mathcal{L}[V_x](j \omega)} = \frac{1}{1+j \omega RC} H ( jω ) = L [ V x ] ( jω ) L [ V y ] ( jω ) = 1 + jω RC 1 となる。カットオフ周波数のパラメータをω c = 1 R C \omega_c = \frac{1}{RC} ω c = RC 1
H ( j ω ) = 1 1 + j ω / ω c H(j \omega) = \frac{1}{1+j \omega / \omega_c} H ( jω ) = 1 + jω / ω c 1 振幅特性と位相特性はそれぞれ次のように書ける。
∣ H ( j ω ) ∣ = ∣ 1 1 + j ω / ω c ∣ arg H ( j ω ) = arg 1 1 + j ω / ω c \begin{aligned}
|H(j \omega)| &= \left| \frac{1}{1+j \omega / \omega_c} \right| \\
\arg H(j \omega) &= \arg \frac{1}{1+j \omega / \omega_c}
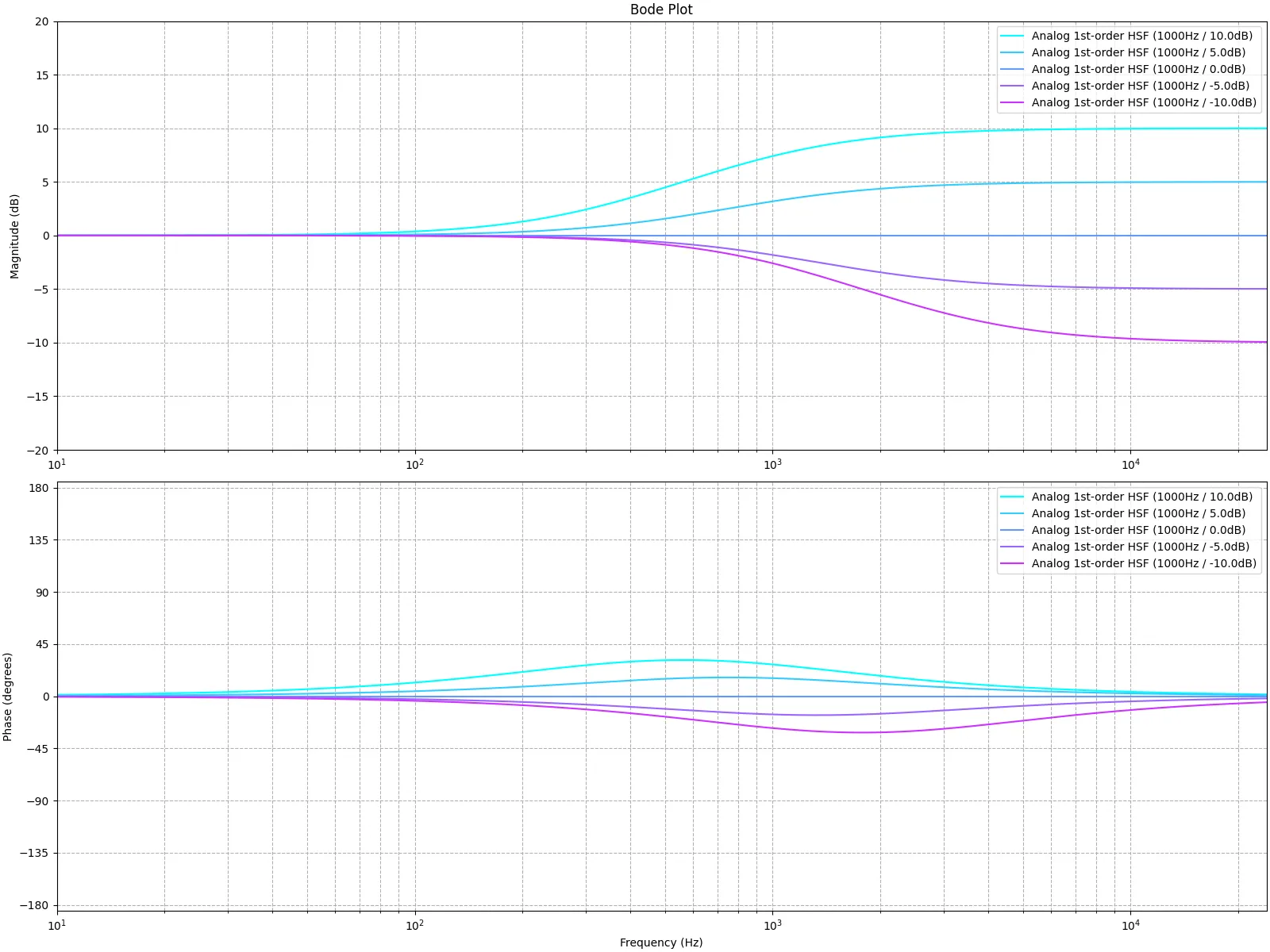
\end{aligned} ∣ H ( jω ) ∣ arg H ( jω ) = 1 + jω / ω c 1 = arg 1 + jω / ω c 1 カットオフ周波数を1000Hzにするために、ω c = 1 R C = 2 π × 1000 \omega_c = \frac{1}{RC} = 2\pi \times 1000 ω c = RC 1 = 2 π × 1000
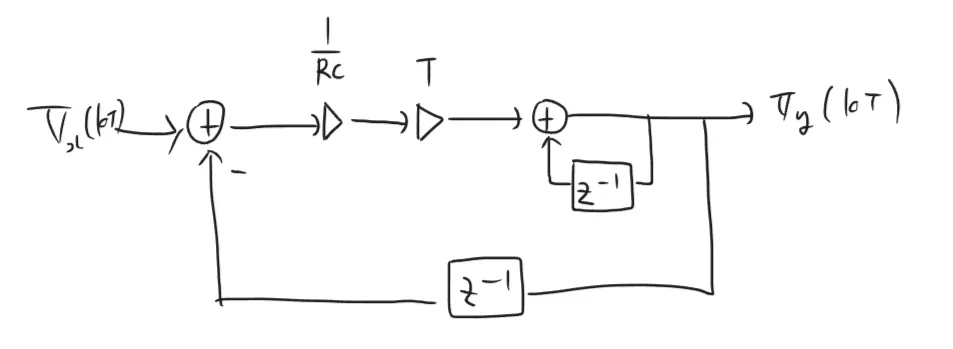
コンピュータ実装のためのブロックダイアグラム
この回路をデジタルフィルタとしてプログラムで実装するために、信号の処理過程を示すブロックダイアグラムを得る。
まず、実際の信号がどのように処理されるのかを知るため、微分方程式を実際に解く。
伝達関数を書き換える。
( 1 + s R C ) L [ V y ] ( s ) = L [ V x ] ( s ) s R C L [ V y ] ( s ) = L [ V x ] ( s ) − L [ V y ] ( s ) L [ V y ] ( s ) = 1 s ⋅ 1 R C ⋅ ( L [ V x ] ( s ) − L [ V y ] ( s ) ) \begin{aligned}
(1+sRC) \mathcal{L}[V_y](s) &= \mathcal{L}[V_x](s)\\
sRC \mathcal{L}[V_y](s) &= \mathcal{L}[V_x](s) - \mathcal{L}[V_y](s) \\
\mathcal{L}[V_y](s) &= \frac{1}{s} \cdot \frac{1}{RC} \cdot (\mathcal{L}[V_x](s) - \mathcal{L}[V_y](s))
\end{aligned} ( 1 + s RC ) L [ V y ] ( s ) s RC L [ V y ] ( s ) L [ V y ] ( s ) = L [ V x ] ( s ) = L [ V x ] ( s ) − L [ V y ] ( s ) = s 1 ⋅ RC 1 ⋅ ( L [ V x ] ( s ) − L [ V y ] ( s )) 逆ラプラス変換を行う。
L [ V y ] ( s ) = 1 s ⋅ 1 R C ⋅ ( L [ V x ] ( s ) − L [ V y ] ( s ) ) = 1 R C ⋅ { 1 s ⋅ L [ V x ] ( s ) − 1 s ⋅ L [ V y ] ( s ) } V y = 1 R C ⋅ { ∫ 0 t V x ( τ ) d τ − ∫ 0 t V y ( τ ) d τ } = 1 R C ⋅ { ∫ 0 t V x ( τ ) − V y ( τ ) d τ } \begin{aligned}
\mathcal{L}[V_y](s) &= \frac{1}{s} \cdot \frac{1}{RC} \cdot (\mathcal{L}[V_x](s) - \mathcal{L}[V_y](s)) \\
&= \frac{1}{RC} \cdot \left\{\frac{1}{s} \cdot \mathcal{L}[V_x](s) - \frac{1}{s} \cdot \mathcal{L}[V_y](s) \right\} \\
V_y &= \frac{1}{RC} \cdot \left\{ \int_0^{t} V_x(\tau) d\tau - \int_0^{t} V_y(\tau) d\tau \right\} \\
&= \frac{1}{RC} \cdot \left\{ \int_0^{t} V_x(\tau) - V_y(\tau) d\tau \right\}
\end{aligned} L [ V y ] ( s ) V y = s 1 ⋅ RC 1 ⋅ ( L [ V x ] ( s ) − L [ V y ] ( s )) = RC 1 ⋅ { s 1 ⋅ L [ V x ] ( s ) − s 1 ⋅ L [ V y ] ( s ) } = RC 1 ⋅ { ∫ 0 t V x ( τ ) d τ − ∫ 0 t V y ( τ ) d τ } = RC 1 ⋅ { ∫ 0 t V x ( τ ) − V y ( τ ) d τ } V x V_x V x V y V_y V y V x V_x V x V y V_y V y V x V_x V x V y V_y V y ∫ 0 t V x ( τ ) − V y ( τ ) d τ \int_0^{t} V_x(\tau) - V_y(\tau) d\tau ∫ 0 t V x ( τ ) − V y ( τ ) d τ T T T
V y ( k T ) = 1 R C ⋅ T { ∑ n = 0 k V x ( n T ) − V y ( n T ) } V_y(kT) = \frac{1}{RC} \cdot T \left\{ \sum_{n=0}^{k} V_x(nT) - V_y(nT) \right\} V y ( k T ) = RC 1 ⋅ T { n = 0 ∑ k V x ( n T ) − V y ( n T ) } これのブロックダイアグラムを考えればゴールだが、積和記号をどのようにブロックダイアグラムにすれば良いのかすぐには分からない。
問題を簡単にし、例としてV y ( t ) = ∫ 0 t V x ( τ ) d τ V_y(t) = \int_0^{t} V_x(\tau) d\tau V y ( t ) = ∫ 0 t V x ( τ ) d τ
V y ( k T ) = T ∑ n = 0 k V x ( n T ) V_y(kT) = T \sum_{n=0}^{k} V_x(nT) V y ( k T ) = T n = 0 ∑ k V x ( n T ) を得る。分かりやすいようにk k k
V y ( 0 ) = T ∑ n = 0 0 V x ( n T ) = T V x ( 0 ) V y ( T ) = T ∑ n = 0 1 V x ( n T ) = T V x ( 0 ) + T V x ( T ) = V y ( 0 ) + T V x ( T ) V y ( 2 T ) = T ∑ n = 0 2 V x ( n T ) = T V x ( 0 ) + T V x ( T ) + T V x ( 2 T ) = V y ( T ) + T V x ( 2 T ) V y ( 3 T ) = T ∑ n = 0 3 V x ( n T ) = T V x ( 0 ) + T V x ( T ) + T V x ( 2 T ) + T V x ( 3 T ) = V y ( 2 T ) + T V x ( 3 T ) ⋯ V y ( k T ) = V y ( ( k − 1 ) T ) + T V x ( k T ) \begin{aligned}
V_y(0) &= T \sum_{n=0}^{0} V_x(nT) = TV_x(0) \\
V_y(T) &= T \sum_{n=0}^{1} V_x(nT) = TV_x(0) + TV_x(T) = V_y(0) + TV_x(T) \\
V_y(2T) &= T \sum_{n=0}^{2} V_x(nT) = TV_x(0) + TV_x(T) + TV_x(2T)= V_y(T) + TV_x(2T) \\
V_y(3T) &= T \sum_{n=0}^{3} V_x(nT) = TV_x(0) + TV_x(T) + TV_x(2T) + TV_x(3T)= V_y(2T) + TV_x(3T) \\
\cdots \\
V_y(kT) &= V_y\left((k-1)T\right) + TV_x(kT)
\end{aligned} V y ( 0 ) V y ( T ) V y ( 2 T ) V y ( 3 T ) ⋯ V y ( k T ) = T n = 0 ∑ 0 V x ( n T ) = T V x ( 0 ) = T n = 0 ∑ 1 V x ( n T ) = T V x ( 0 ) + T V x ( T ) = V y ( 0 ) + T V x ( T ) = T n = 0 ∑ 2 V x ( n T ) = T V x ( 0 ) + T V x ( T ) + T V x ( 2 T ) = V y ( T ) + T V x ( 2 T ) = T n = 0 ∑ 3 V x ( n T ) = T V x ( 0 ) + T V x ( T ) + T V x ( 2 T ) + T V x ( 3 T ) = V y ( 2 T ) + T V x ( 3 T ) = V y ( ( k − 1 ) T ) + T V x ( k T ) これからブロックダイアグラムを書くと、
z − 1 z^{-1} z − 1
これを使えば、先の式のダイアグラムを書くことができる。
V y ( k T ) = 1 R C ⋅ T { ∑ n = 0 k V x ( n T ) − V y ( n T ) } \begin{aligned}
V_y(kT) &= \frac{1}{RC} \cdot T \left\{ \sum_{n=0}^{k} V_x(nT) - V_y(nT) \right\} \\
\end{aligned} V y ( k T ) = RC 1 ⋅ T { n = 0 ∑ k V x ( n T ) − V y ( n T ) }
これをプログラムで実装すれば、デジタルフィルタを実現できる。
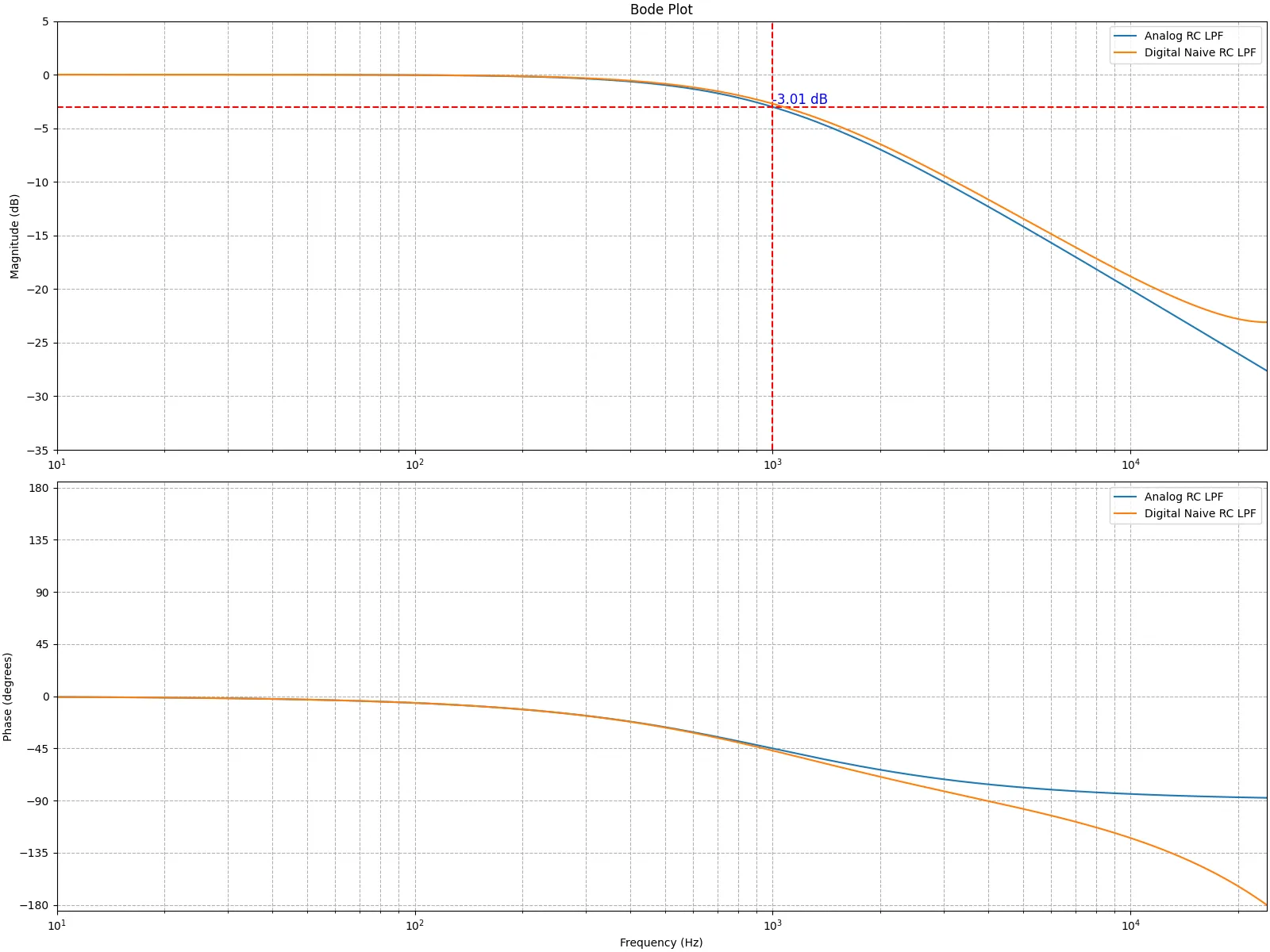
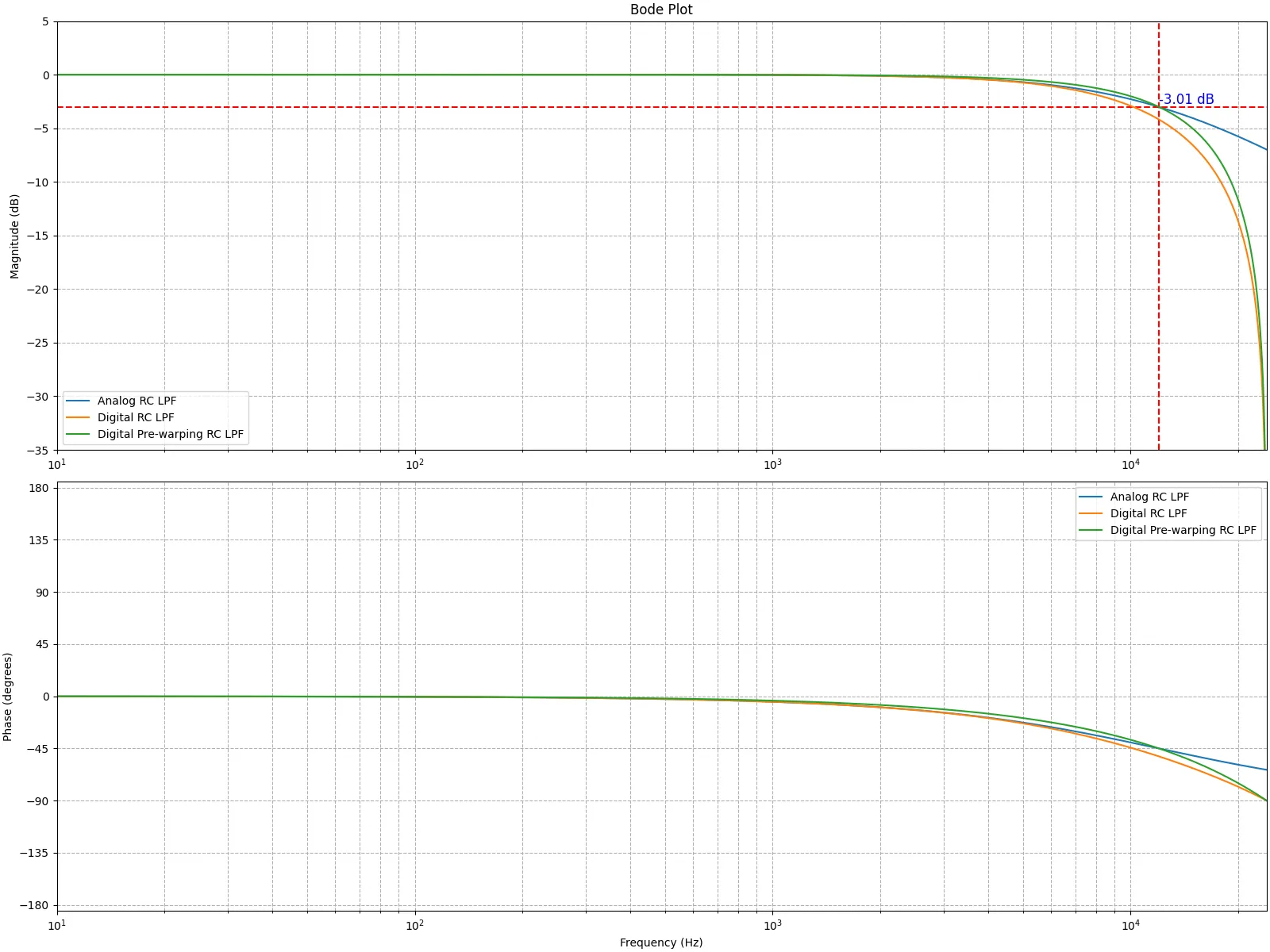
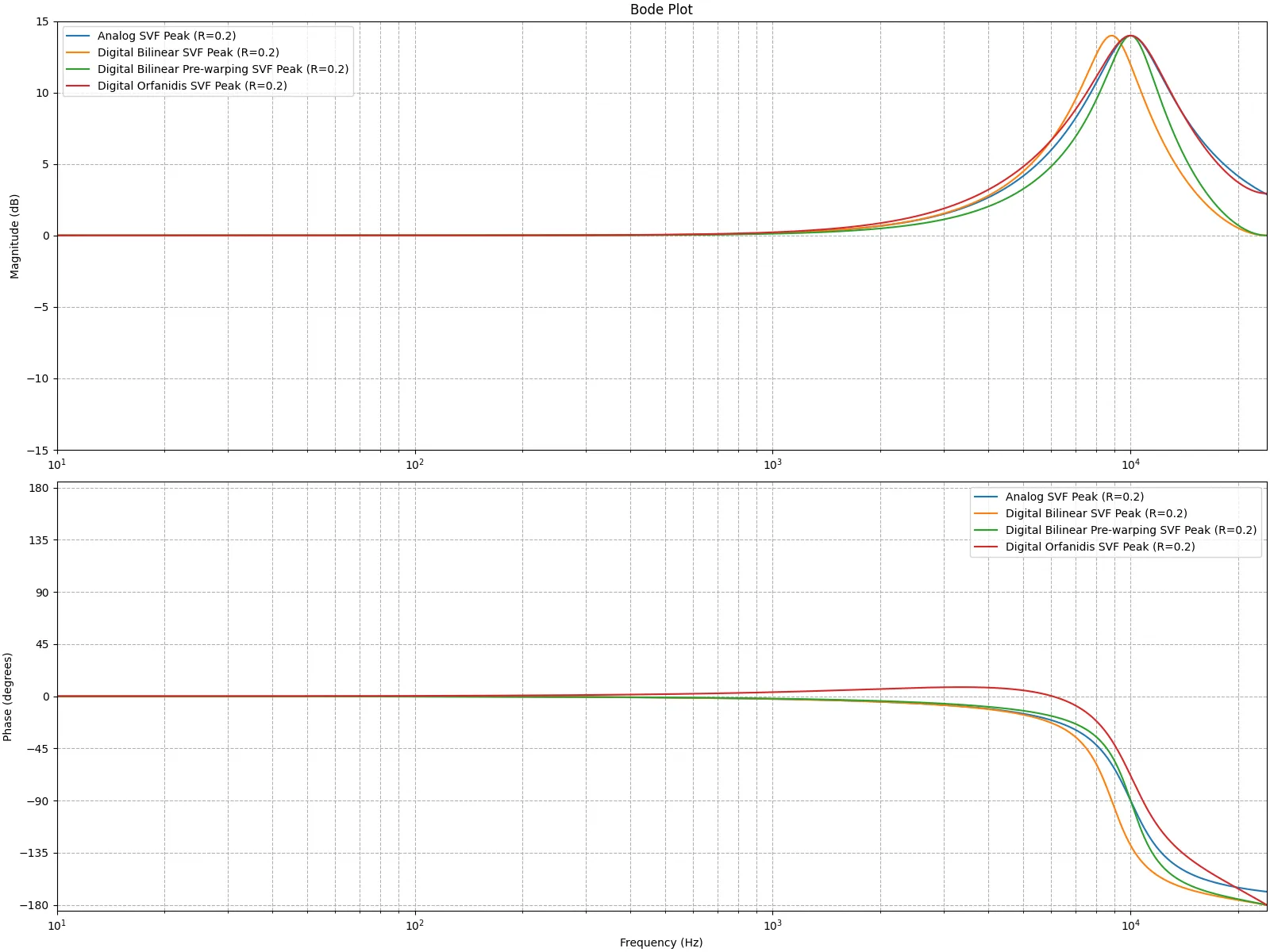
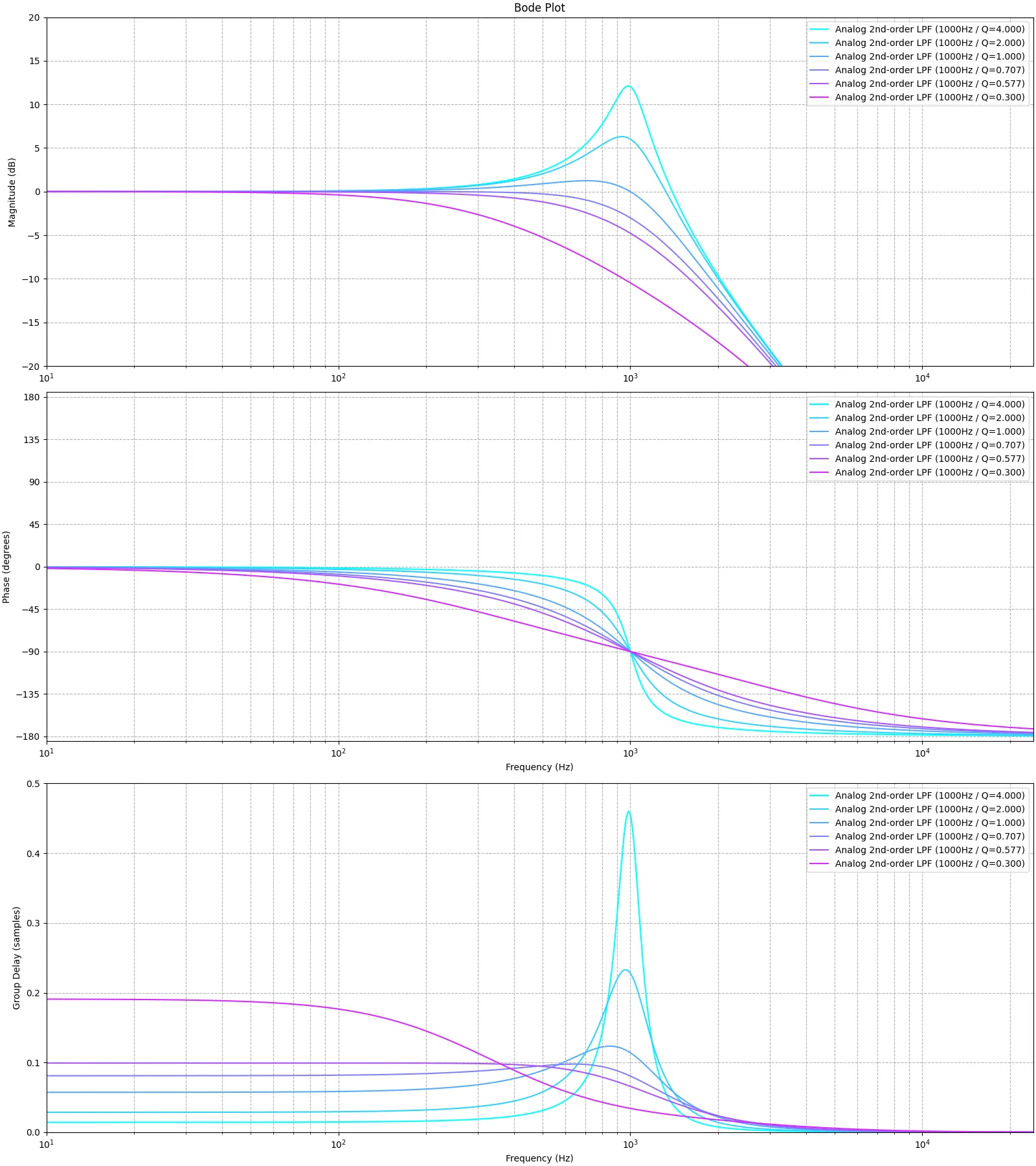
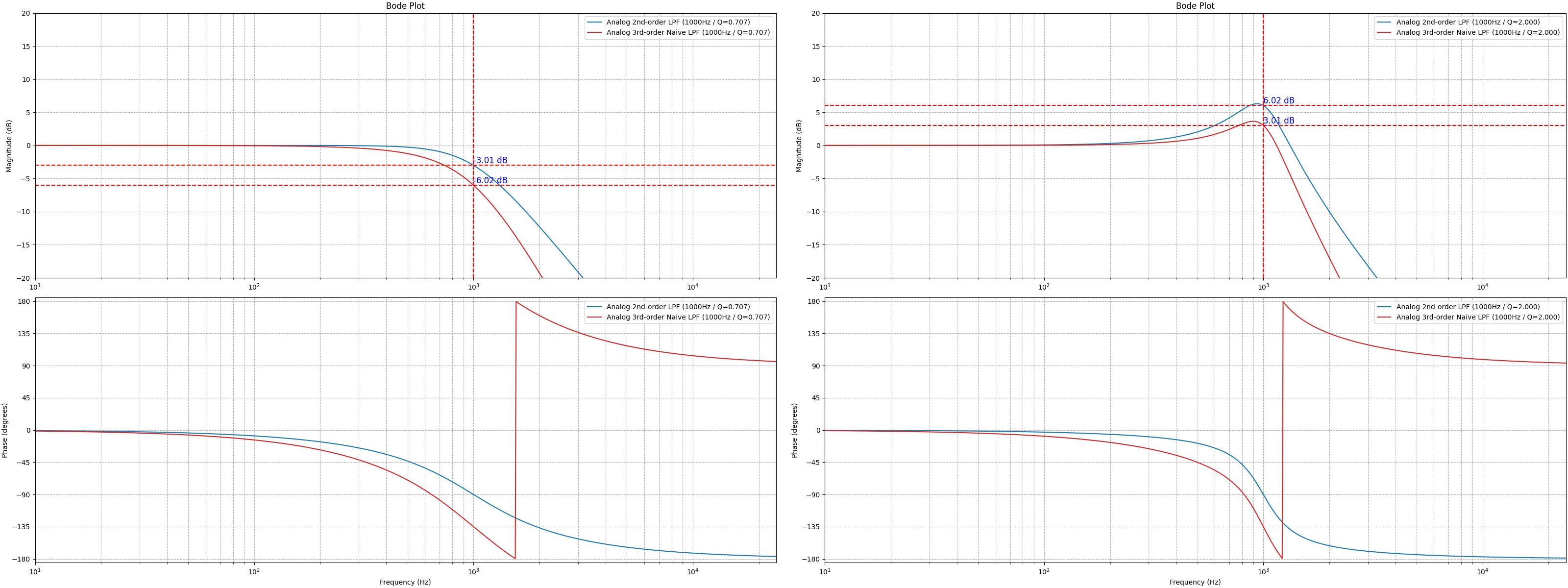
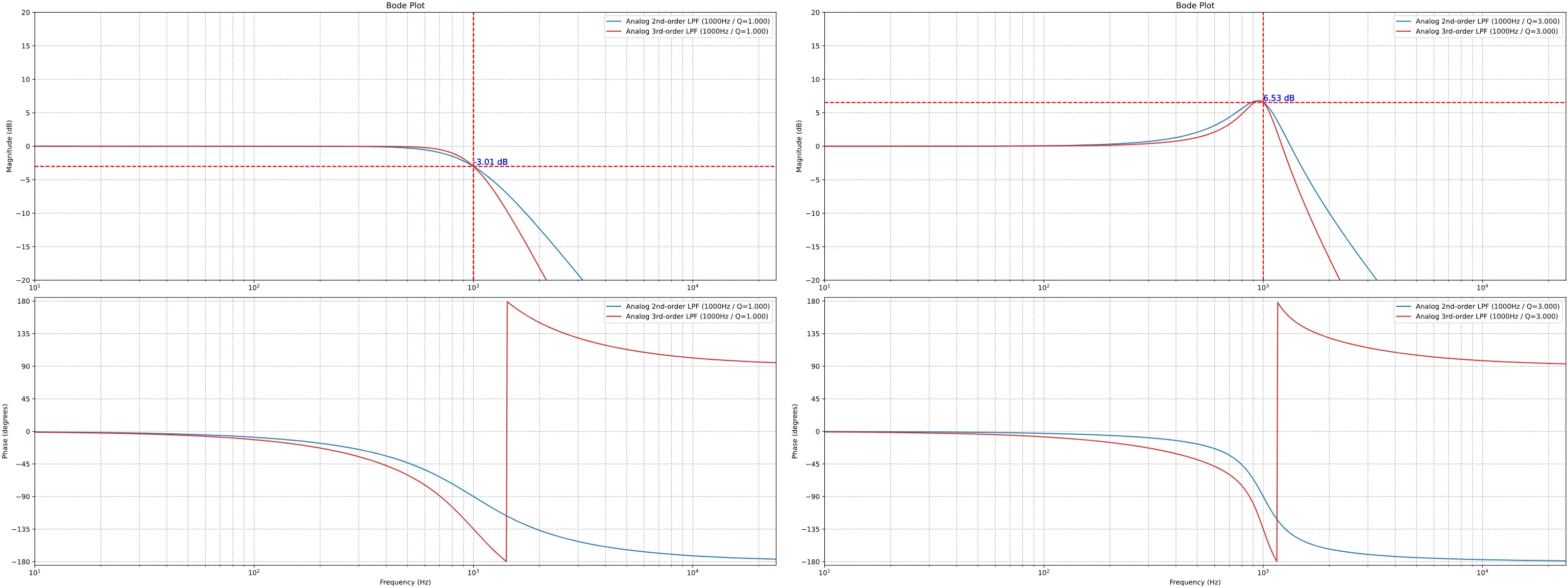
カットオフ周波数が1000Hzになるようにパラメータを設定して実装し、振幅特性と位相特性を図示すると下記のようになる。サンプリング周波数は48000Hzである。青色で示されるAnalog RC LPFがアナログフィルタの特性を示し、橙色のDigital Naive RC LPFが上記ダイアグラムを実装して作ったデジタルフィルタの特性である。ナイキスト周波数に近づくにつれてアナログフィルタの特性と乖離していることが分かる。
双一次変換法
デジタルフィルタをアナログフィルタ電気回路から直接設計する手法はあまり効率的ではない。出来れば、アナログフィルタの伝達関数を良い感じに変形すればデジタルフィルタを得られるようにしたい。その方法が双一次変換法である。
標本化定理の所で扱ったように、連続時間信号の周波数領域は − ∞ ∼ ∞ -\infty \sim \infty − ∞ ∼ ∞ − π T ∼ π T -\frac{\pi}{T} \sim \frac{\pi}{T} − T π ∼ T π − ∞ ∼ ∞ -\infty \sim \infty − ∞ ∼ ∞ − π T ∼ π T -\frac{\pi}{T} \sim \frac{\pi}{T} − T π ∼ T π
アナログフィルタの伝達関数から周波数特性を得るにはs = j ω s=j\omega s = jω s s s z = e j ω z=e^{j\omega} z = e jω z z z s s s z z z s = 1 − z − 1 1 + z − 1 s=\frac{1-z^{-1}}{1+z^{-1}} s = 1 + z − 1 1 − z − 1
双一次変換法は、アナログフィルタの解析の結果得た伝達関数H ( s ) H(s) H ( s ) s = 1 − z − 1 1 + z − 1 s=\frac{1-z^{-1}}{1+z^{-1}} s = 1 + z − 1 1 − z − 1 s = j Ω s = j\Omega s = j Ω z = e j ω T z = e^{j\omega T} z = e jω T H ( s ) H(s) H ( s ) H ( 1 − e − j ω T 1 + e − j ω T ) H\left( \frac{1-e^{-j \omega T}}{1+e^{-j \omega T}} \right) H ( 1 + e − jω T 1 − e − jω T ) H ( j Ω ) H(j\Omega) H ( j Ω ) H ( 1 − e − j ω T 1 + e − j ω T ) H\left( \frac{1-e^{-j \omega T}}{1+e^{-j \omega T}} \right) H ( 1 + e − jω T 1 − e − jω T ) Ω \Omega Ω ω \omega ω
j Ω = 1 − e − j ω T 1 + e − j ω T = tanh ( j ω T 2 ) = j tan ω T 2 Ω = tan ω T 2 \begin{aligned}
j \Omega &= \frac{1-e^{-j \omega T}}{1+e^{-j \omega T}} = \tanh \left( j\frac{\omega T}{2} \right) = j \tan \frac{\omega T}{2} \\
\Omega &= \tan \frac{\omega T}{2}
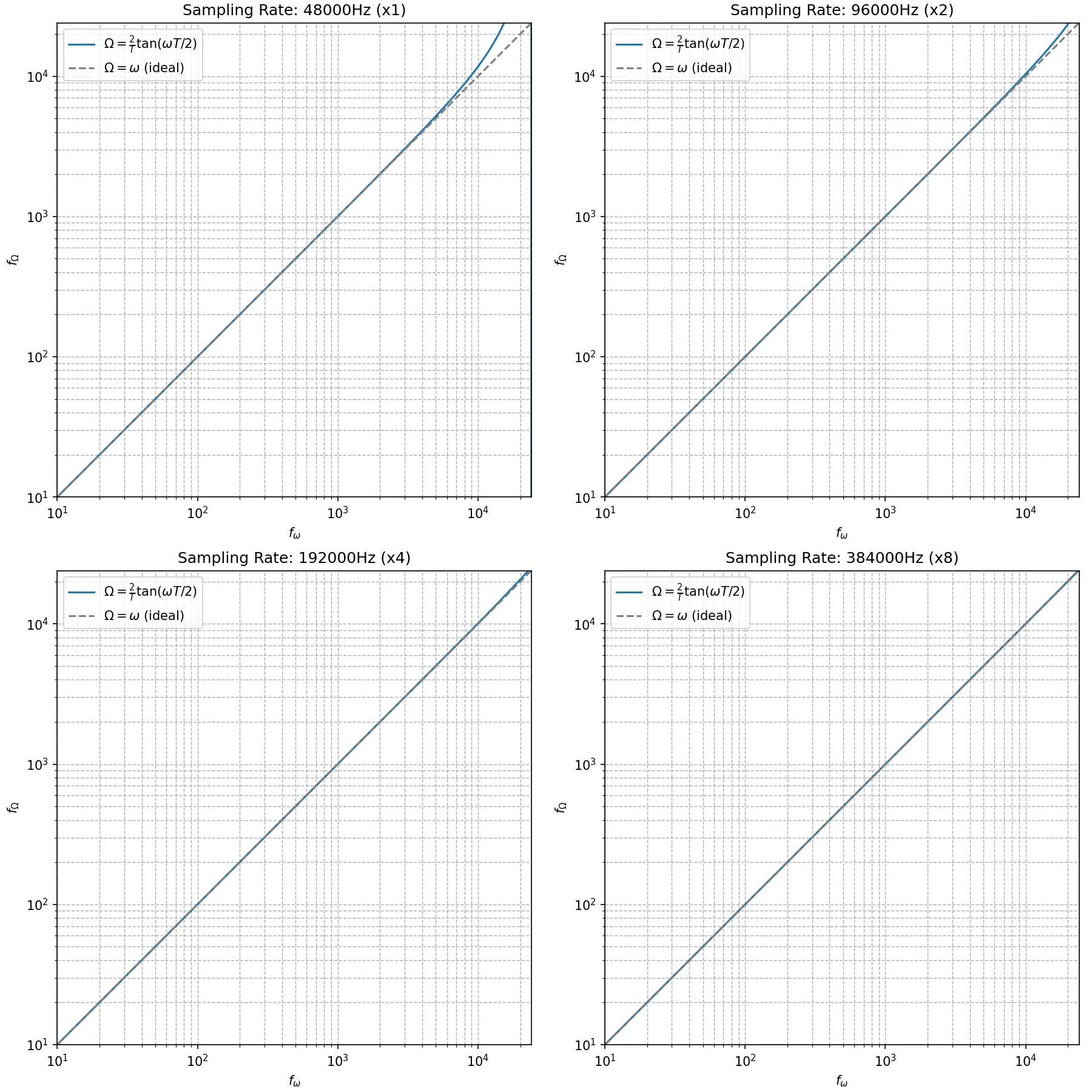
\end{aligned} j Ω Ω = 1 + e − jω T 1 − e − jω T = tanh ( j 2 ω T ) = j tan 2 ω T = tan 2 ω T となる。つまり対応関係が非線形であり、周波数尺度が変わってしまう。この対応関係を多少まともにする方法として、双一次変換の際にアナログフィルタの伝達関数H ( s ) H(s) H ( s ) s = 2 T 1 − z − 1 1 + z − 1 s=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}} s = T 2 1 + z − 1 1 − z − 1
これにより、アナログ領域のΩ \Omega Ω ω \omega ω
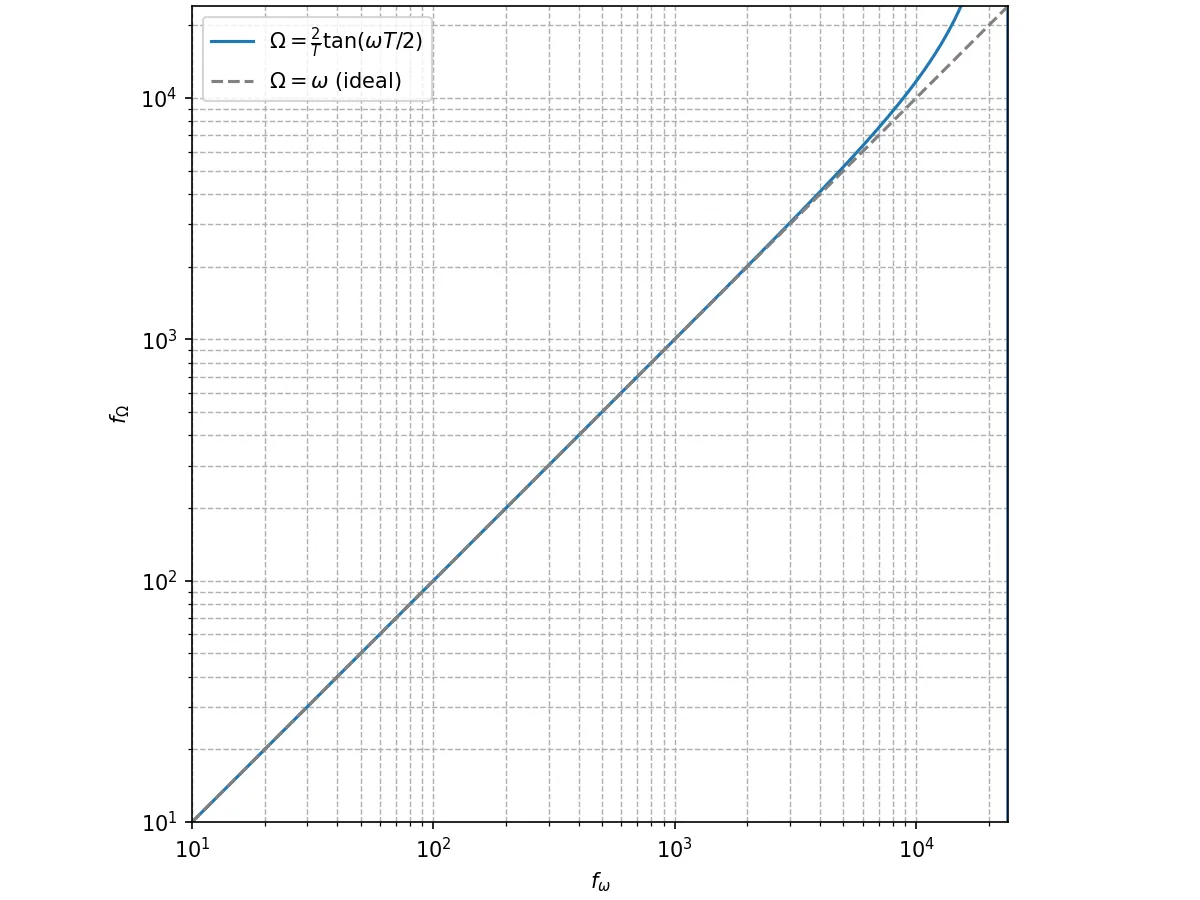
Ω = 2 T tan ω T 2 \begin{aligned}
\Omega &= \frac{2}{T} \tan \frac{\omega T}{2}
\end{aligned} Ω = T 2 tan 2 ω T となる。この関係を、角周波数を周波数に変更して対数軸にプロットした物が下図である。サンプリング周波数は48000Hzとしている。このグラフから、Ω \Omega Ω ω \omega ω Ω = ω \Omega=\omega Ω = ω
実際に双一次変換法を用いて、先に説明したRC低域通過フィルタの伝達関数からデジタルフィルタを得てみよう。
RC低域通過フィルタの伝達関数は次の通り。
H ( s ) = 1 1 + s R C H(s) = \frac{1}{1+sRC} H ( s ) = 1 + s RC 1 s = 2 T 1 − z − 1 1 + z − 1 s=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}} s = T 2 1 + z − 1 1 − z − 1
H ( z ) = 1 1 + R C 2 T 1 − z − 1 1 + z − 1 = T + T z − 1 T + T z − 1 + 2 R C − 2 R C z − 1 = T + T z − 1 ( T + 2 R C ) + ( T − 2 R C ) z − 1 = T T + 2 R C + T T + 2 R C z − 1 1 + T − 2 R C T + 2 R C z − 1 \begin{aligned}
H(z) &= \frac{1}{1+RC \frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}} \\
&= \frac{T + Tz^{-1}}{T + Tz^{-1} + 2RC- 2RCz^{-1}} \\
&= \frac{T + Tz^{-1}}{(T + 2RC) + (T - 2RC)z^{-1}} \\
&= \frac{\frac{T}{T + 2RC} + \frac{T}{T + 2RC}z^{-1}}{1 + \frac{T - 2RC}{T + 2RC}z^{-1}} \\
\end{aligned} H ( z ) = 1 + RC T 2 1 + z − 1 1 − z − 1 1 = T + T z − 1 + 2 RC − 2 RC z − 1 T + T z − 1 = ( T + 2 RC ) + ( T − 2 RC ) z − 1 T + T z − 1 = 1 + T + 2 RC T − 2 RC z − 1 T + 2 RC T + T + 2 RC T z − 1 離散時間信号の差分方程式が
y ( n T ) = ∑ k = 0 M a k x ( n T − k T ) − ∑ k = 1 N b k y ( n T − k T ) \begin{aligned}
y(nT) &= \sum_{k=0}^{M} a_k x(nT-kT) - \sum_{k=1}^{N}b_ky(nT-kT) \\
\end{aligned} y ( n T ) = k = 0 ∑ M a k x ( n T − k T ) − k = 1 ∑ N b k y ( n T − k T ) である時、そのZ変換が
Y ( z ) X ( z ) = ∑ k = 0 M a k z − k 1 + ∑ k = 1 N b k z − k \begin{aligned}
\frac{Y(z)}{X(z)} &= \frac{\sum_{k=0}^{M} a_k z^{-k}}{1+\sum_{k=1}^{N} b_k z^{-k}}
\end{aligned} X ( z ) Y ( z ) = 1 + ∑ k = 1 N b k z − k ∑ k = 0 M a k z − k なので、係数a 0 , a 1 , b 1 a_0, a_1, b_1 a 0 , a 1 , b 1
a 0 = T T + 2 R C , a 1 = T T + 2 R C , b 1 = T − 2 R C T + 2 R C a_0 = \frac{T}{T + 2RC}, \quad
a_1 = \frac{T}{T + 2RC}, \quad
b_1 = \frac{T - 2RC}{T + 2RC} a 0 = T + 2 RC T , a 1 = T + 2 RC T , b 1 = T + 2 RC T − 2 RC である。
RC低域通過フィルタは1次のフィルタなので、改めて差分方程式を書くと、
y ( n T ) = a 0 x ( n T ) + a 1 x ( n T − T ) − b 1 y ( n T − T ) \begin{aligned}
y(nT) &= a_0 x(nT) + a_1 x(nT-T) - b_1 y(nT-T)
\end{aligned} y ( n T ) = a 0 x ( n T ) + a 1 x ( n T − T ) − b 1 y ( n T − T ) である。
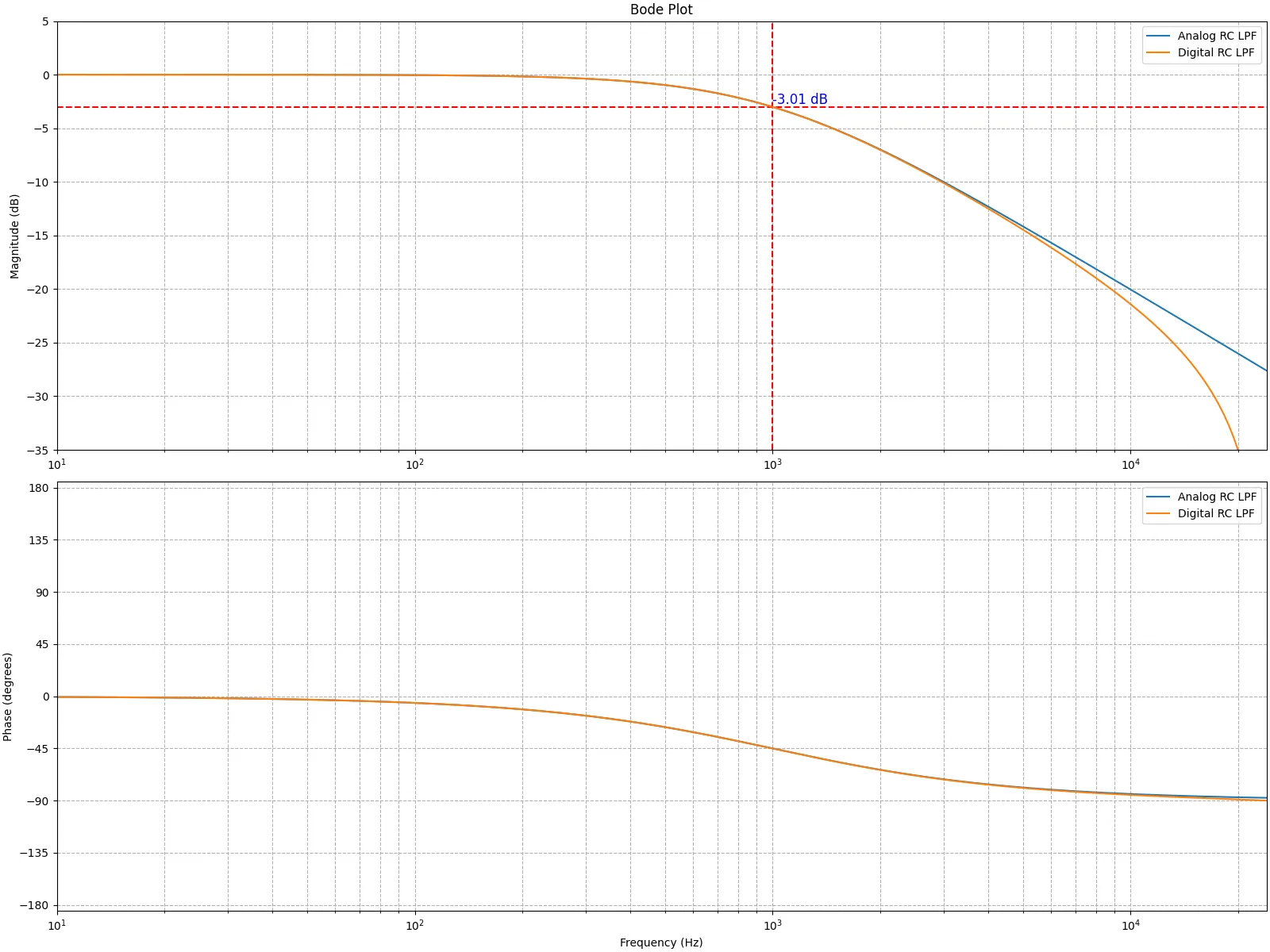
カットオフ周波数が1000Hzになるようにパラメータを設定して実装し、振幅特性と位相特性を図示すると下記のようになる。サンプリング周波数は48000Hzである。青色で示されるAnalog RC LPFがアナログフィルタの特性を示し、橙色のDigital RC LPFが上記を実装して作ったデジタルフィルタの特性である。
概ね形がアナログフィルタに近いもののナイキスト周波数に近づくにつれてずれ始めることが分かる。
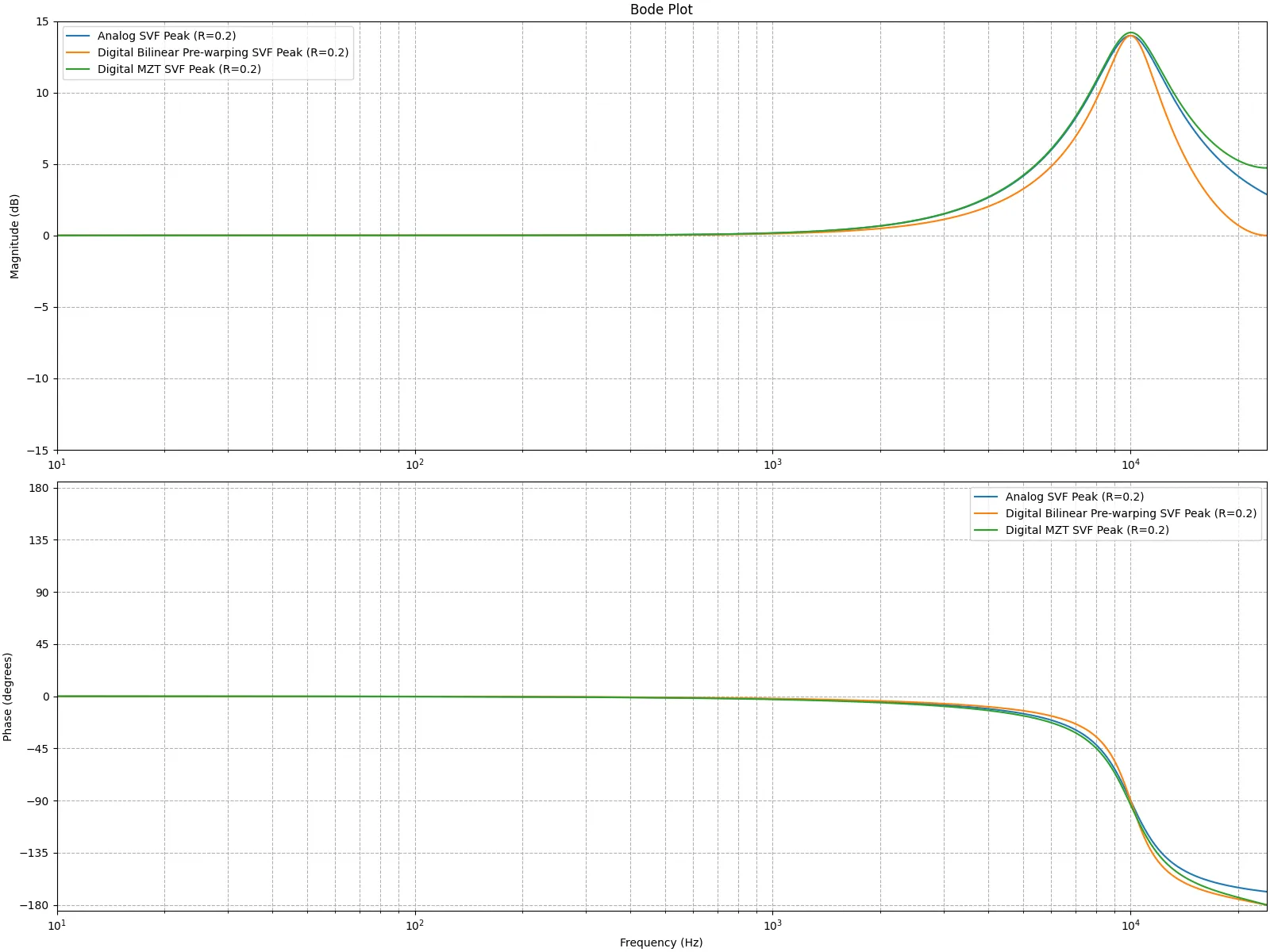
更にカットオフ周波数を高くすると、指定した周波数より早く減衰が始まってしまう。そこでΩ = 2 T tan ω T 2 \Omega = \frac{2}{T} \tan \frac{\omega T}{2} Ω = T 2 tan 2 ω T Ω \Omega Ω
その他の著名な方法(Orfanidis)
双一次変換法は非常に便利だが、オーディオ信号処理においては割と致命的な欠陥を持つ。そこで非常に多くの研究が行われてきた。ここでは比較的有名な研究を紹介する。
1つ目が1997年のS.J.Orfanidisによる研究である。
S. J. Orfanidis, “Digital parametric equalizer design with prescribed Nyquist-frequency gain,” Journal of the Audio Engineering Society, vol. 45, no. 6, pp. 444-455, Jun. 1997.
ナイキスト周波数に近づくにつれてどんどん減衰して行ってしまうので、その分ゲインして補正してあげようというアイデアである。
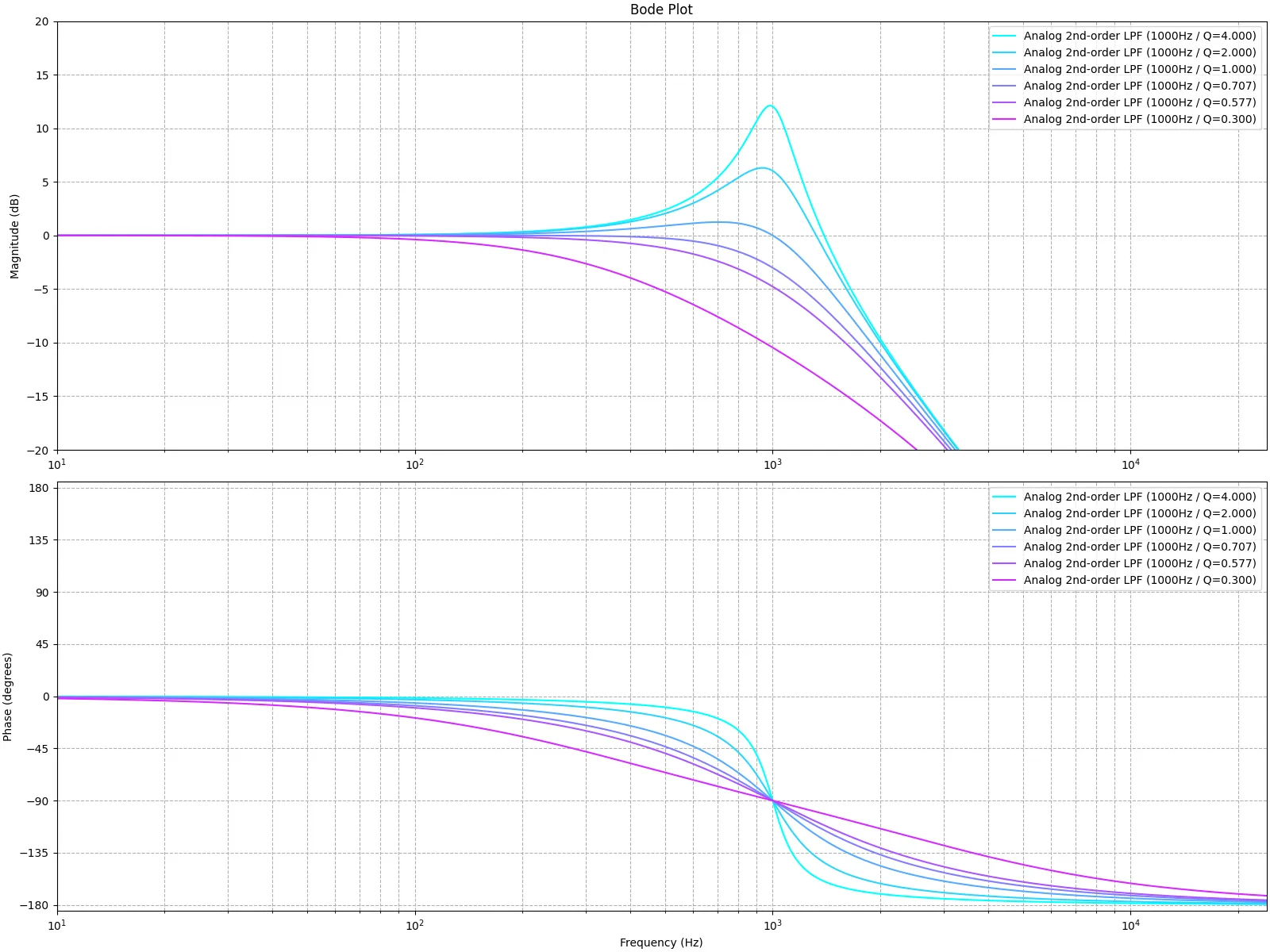
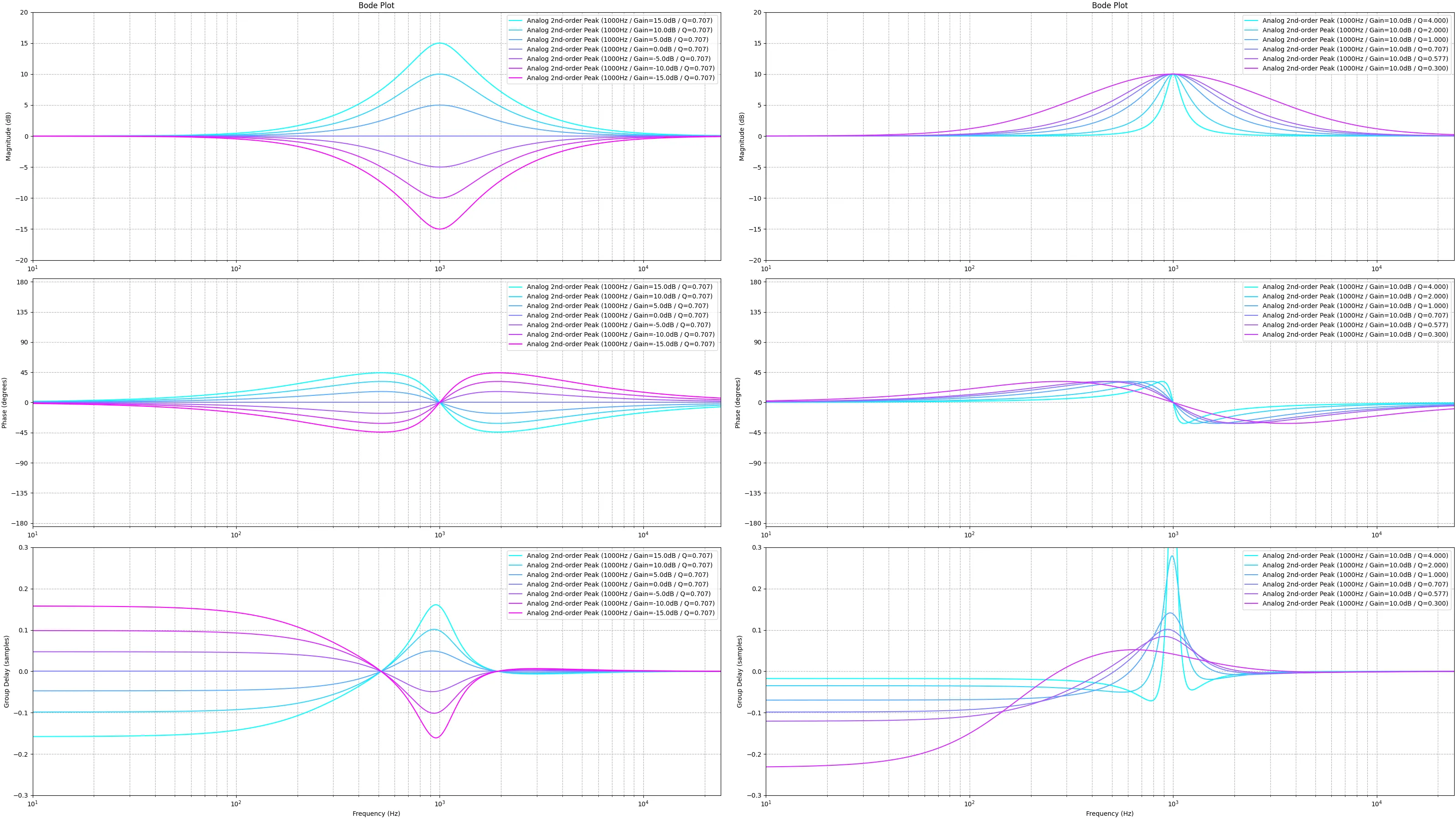
Orfanidisの手法は2次のピークフィルタでのみ利用できる。詳しくは後述するが、高次のフィルタも演算誤差を抑える為に2次以下のフィルタの連結で表現することが普通であるため、2次フィルタのみ可という制約はそれほど甚大ではない。ベル型以外のフィルターは別の方法を適用する。
まず、ゲインが DC(f = 0 [ H z ] f=0\,[\mathrm{Hz}] f = 0 [ Hz ] f = ∞ [ H z ] f=\infty\,[\mathrm{Hz}] f = ∞ [ Hz ] G 0 G_0 G 0 Ω 0 \Omega_0 Ω 0 A , B A,\ B A , B
H ( s ) = G 0 s 2 + B s + G 0 Ω 0 2 s 2 + A s + Ω 0 2 H(s) = \frac{G_0 s^2 + B s + G_0 \Omega_0^2}{s^2 + A s + \Omega_0^2} H ( s ) = s 2 + A s + Ω 0 2 G 0 s 2 + B s + G 0 Ω 0 2 のように表せる。なおA , B A,\ B A , B Ω 0 \Omega_0 Ω 0 G G G Δ Ω \Delta \Omega ΔΩ G B G_B G B
A = G B 2 − G 0 2 G 2 − G B 2 Δ Ω , B = G A A = \sqrt{\frac{G_B^2 - G_0^2}{G^2 - G_B^2}} \Delta\Omega, \quad B = G A A = G 2 − G B 2 G B 2 − G 0 2 ΔΩ , B = G A
ここから、ナイキスト周波数がG 1 G_1 G 1 f = ∞ [ H z ] f=\infty\,[\mathrm{Hz}] f = ∞ [ Hz ] G 1 G_1 G 1
H ( s ) = G 1 s 2 + B s + G 0 W 2 s 2 + A s + W 2 H(s) = \frac{G_1 s^2 + B s + G_0 W^2}{s^2 + A s + W^2} H ( s ) = s 2 + A s + W 2 G 1 s 2 + B s + G 0 W 2 の係数を求める。詳細な導出は元論文を辿って欲しい。結論を述べると、
W 2 = G 2 − G 1 2 G 2 − G 0 2 Ω 0 2 , A = C + D ∣ G 2 − G B 2 ∣ , B = G 2 C + G B 2 D ∣ G 2 − G B 2 ∣ C = ( Δ Ω ) 2 ∣ G B 2 − G 1 2 ∣ − 2 W 2 ( ∣ G B 2 − G 0 G 1 ∣ − ( G B 2 − G 0 2 ) ( G B 2 − G 1 2 ) ) D = 2 W 2 ( ∣ G 2 − G 0 G 1 ∣ − ( G 2 − G 0 2 ) ( G 2 − G 1 2 ) ) W^2 = \sqrt{\frac{G^2 - G_1^2}{G^2 - G_0^2}} \Omega_0^2, \quad
A = \sqrt{\frac{C + D}{|G^2 - G_B^2|}}, \quad
B = \sqrt{\frac{G^2 C + G_B^2 D}{|G^2 - G_B^2|}} \\
C = (\Delta\Omega)^2 |G_B^2 - G_1^2| - 2W^2 \left( |G_B^2 - G_0 G_1| - \sqrt{(G_B^2 - G_0^2)(G_B^2 - G_1^2)} \right) \\
D = 2W^2 \left( |G^2 - G_0 G_1| - \sqrt{(G^2 - G_0^2)(G^2 - G_1^2)} \right) W 2 = G 2 − G 0 2 G 2 − G 1 2 Ω 0 2 , A = ∣ G 2 − G B 2 ∣ C + D , B = ∣ G 2 − G B 2 ∣ G 2 C + G B 2 D C = ( ΔΩ ) 2 ∣ G B 2 − G 1 2 ∣ − 2 W 2 ( ∣ G B 2 − G 0 G 1 ∣ − ( G B 2 − G 0 2 ) ( G B 2 − G 1 2 ) ) D = 2 W 2 ( ∣ G 2 − G 0 G 1 ∣ − ( G 2 − G 0 2 ) ( G 2 − G 1 2 ) ) である。これに双一次変換を適応して、以下を得る。
H ( z ) = ( G 1 + G 0 W 2 + B 1 + W 2 + A ) − 2 ( G 1 − G 0 W 2 1 + W 2 + A ) z − 1 + ( G 1 + G 0 W 2 − B 1 + W 2 + A ) z − 2 1 − 2 ( 1 − W 2 1 + W 2 + A ) z − 1 + ( 1 + W 2 − A 1 + W 2 + A ) z − 2 H(z) = \frac{\left( \frac{G_1+G_0W^2+B}{1+W^2+A} \right) -2 \left( \frac{G_1-G_0W^2}{1+W^2+A} \right)z^{-1} + \left( \frac{G_1+G_0W^2-B}{1+W^2+A} \right)z^{-2}}{1-2\left( \frac{1-W^2}{1+W^2+A} \right)z^{-1} + \left( \frac{1+W^2-A}{1+W^2+A} \right)z^{-2}} H ( z ) = 1 − 2 ( 1 + W 2 + A 1 − W 2 ) z − 1 + ( 1 + W 2 + A 1 + W 2 − A ) z − 2 ( 1 + W 2 + A G 1 + G 0 W 2 + B ) − 2 ( 1 + W 2 + A G 1 − G 0 W 2 ) z − 1 + ( 1 + W 2 + A G 1 + G 0 W 2 − B ) z − 2 なお双一次変換はs = 1 − z − 1 1 + z − 1 s=\frac{1-z^{-1}}{1+z^{-1}} s = 1 + z − 1 1 − z − 1 f 0 [ H z ] f_0\, \mathrm{[Hz]} f 0 [ Hz ] f s [ H z ] f_s\, \mathrm{[Hz]} f s [ Hz ] ω 0 = 2 π f 0 f s , Δ ω = 2 π Δ f f s \omega_0 = \frac{2 \pi f_0}{f_s}, \Delta \omega = \frac{2 \pi \Delta f}{f_s} ω 0 = f s 2 π f 0 , Δ ω = f s 2 π Δ f
Ω 0 = tan ( ω 0 2 ) , Δ Ω = ( 1 + G B 2 − G 0 2 G B 2 − G 1 2 G 2 − G 1 2 G 2 − G 0 2 Ω 0 2 ) tan ( Δ ω 2 ) \Omega_0 = \tan \left( \frac{\omega_0}{2} \right), \quad \Delta \Omega = \left( 1 + \sqrt{\frac{G_B^2 - G_0^2}{G_B^2 - G_1^2}} \sqrt{\frac{G^2 - G_1^2}{G^2 - G_0^2}} \Omega_0^2 \right) \tan \left( \frac{\Delta \omega}{2} \right) Ω 0 = tan ( 2 ω 0 ) , ΔΩ = ( 1 + G B 2 − G 1 2 G B 2 − G 0 2 G 2 − G 0 2 G 2 − G 1 2 Ω 0 2 ) tan ( 2 Δ ω ) とする。
実際にこの手法を用いてみよう。アナログ2次ピークフィルタの一例として、次のような伝達関数を持つものを考える。R R R
H ( s ) = Ω 0 2 − s 2 s 2 + 2 R Ω 0 s + Ω 0 2 H(s) = \frac{\Omega_0^2-s^2}{s^2+2R\Omega_0s+\Omega_0^2} H ( s ) = s 2 + 2 R Ω 0 s + Ω 0 2 Ω 0 2 − s 2
まずW W W G G G G 0 , G 1 G_0,\ G_1 G 0 , G 1 G G G s = j Ω 0 s=j\Omega_0 s = j Ω 0
G = ∣ H ( j Ω 0 ) ∣ = ∣ Ω 0 2 − ( j Ω 0 ) 2 ( j Ω 0 ) 2 + 2 R Ω 0 ( j Ω 0 ) + Ω 0 2 ∣ = 1 R \begin{aligned}
G=|H(j\Omega_0)| &=\left| \frac{\Omega_0^2-(j\Omega_0)^2}{(j\Omega_0)^2+2R\Omega_0(j\Omega_0)+\Omega_0^2} \right| \\
&= \frac{1}{R}
\end{aligned} G = ∣ H ( j Ω 0 ) ∣ = ( j Ω 0 ) 2 + 2 R Ω 0 ( j Ω 0 ) + Ω 0 2 Ω 0 2 − ( j Ω 0 ) 2 = R 1 G 0 G_0 G 0 ∣ H ( 0 ) ∣ |H(0)| ∣ H ( 0 ) ∣
G 0 = ∣ H ( 0 ) ∣ = 1 G_0 = |H(0)| = 1 G 0 = ∣ H ( 0 ) ∣ = 1 G 1 G_1 G 1 f 0 [ H z ] f_0\, \mathrm{[Hz]} f 0 [ Hz ] f s [ H z ] f_s\, \mathrm{[Hz]} f s [ Hz ] ω 0 = 2 π f 0 f s , Δ ω = 2 π Δ f f s \omega_0 = \frac{2 \pi f_0}{f_s}, \Delta \omega = \frac{2 \pi \Delta f}{f_s} ω 0 = f s 2 π f 0 , Δ ω = f s 2 π Δ f
G 1 2 = G 0 2 ( ω 0 2 − π 2 ) 2 + G 2 π 2 ( Δ ω ) 2 ( G B 2 − G 0 2 ) / ( G 2 − G B 2 ) ( ω 0 2 − π 2 ) 2 + π 2 ( Δ ω ) 2 ( G B 2 − G 0 2 ) / ( G 2 − G B 2 ) G_1^2 = \frac{ G_0^2 (\omega_0^2 - \pi^2)^2 + G^2 \pi^2 (\Delta \omega)^2 \left( G_B^2 - G_0^2 \right) / \left( G^2 - G_B^2 \right) }{ (\omega_0^2 - \pi^2)^2 + \pi^2 (\Delta \omega)^2 \left( G_B^2 - G_0^2 \right) / \left( G^2 - G_B^2 \right) } G 1 2 = ( ω 0 2 − π 2 ) 2 + π 2 ( Δ ω ) 2 ( G B 2 − G 0 2 ) / ( G 2 − G B 2 ) G 0 2 ( ω 0 2 − π 2 ) 2 + G 2 π 2 ( Δ ω ) 2 ( G B 2 − G 0 2 ) / ( G 2 − G B 2 ) 続いて、A A A G B G_B G B Δ Ω \Delta\Omega ΔΩ G B = G 0 G G_B=\sqrt{G_0G} G B = G 0 G
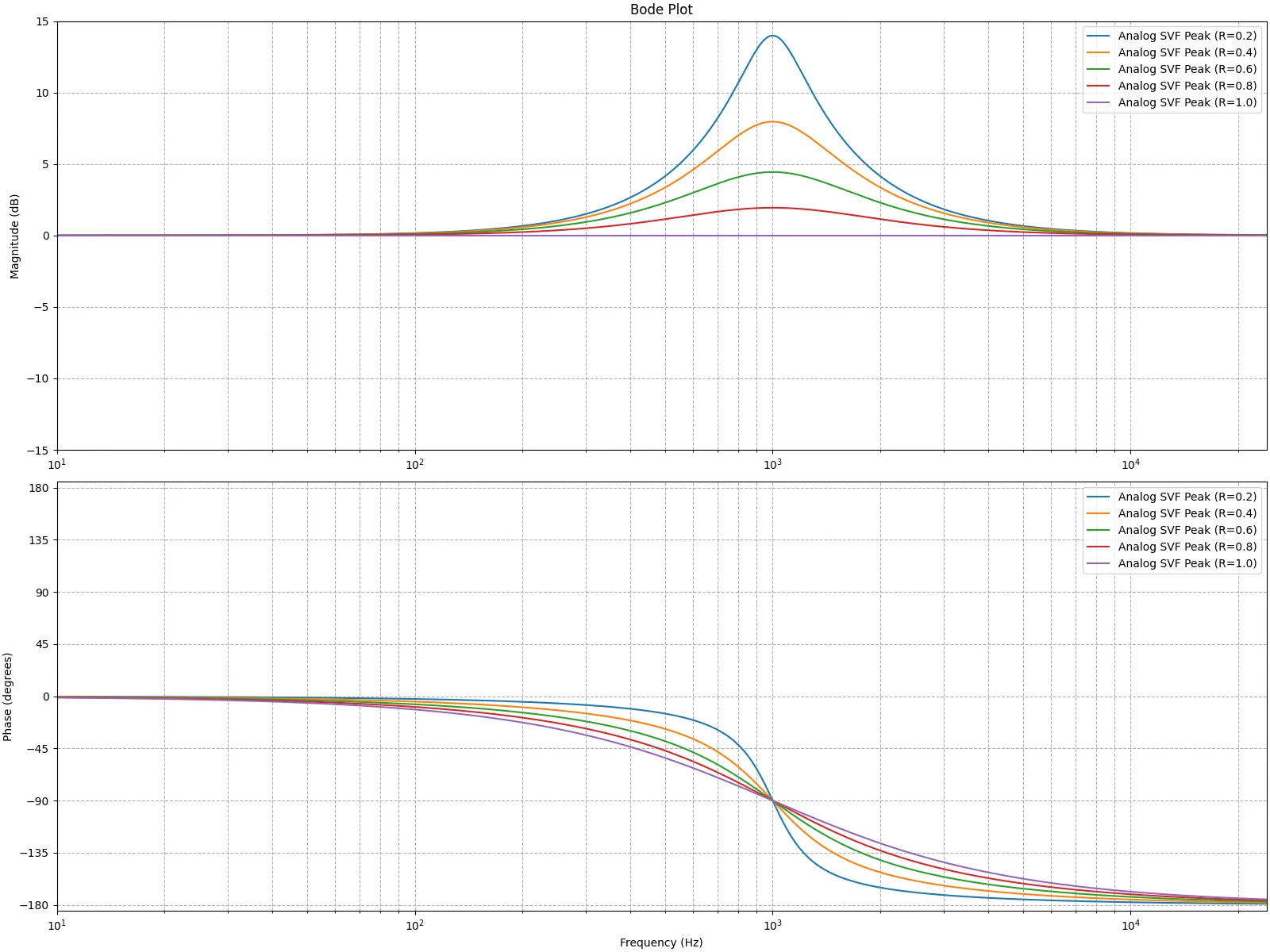
サンプリング周波数を48000Hz、中心周波数を10000Hz、R = 0.2 R=0.2 R = 0.2
その他の著名な方法(MZTi)
D. W. Gunness and O. S. Chauhan, “Optimizing the magnitude response of matched z-transform filters (“mzti”) for loudspeaker equalization”, journal of the audio engineering society, no. 2, Sep. 2007.
Orfanidisの手法は、通常の双一次変換と比較して大きな改善を達成している。しかし、いくつか問題がある。まず、位相特性がアナログフィルタと大きく異なっている。そして、ナイキスト周波数付近の振幅特性がアナログフィルタと一致するようにデジタルフィルタを設計したが、通常、ナイキスト周波数付近の音は聴覚できない。また、リサンプリングの際に用いるアンチエイリアシングフィルタはナイキスト周波数付近のゲインをゼロに向かわせるため、そこでの特性を一致させることには意味がない。更に、聴覚可能な周波数帯域において、アナログフィルタとの特性の乖離が生じており、問題である。MZTiは、この課題意識から生まれた手法である。
前々節では、アナログフィルタをデジタルフィルタに変換する方法として双一次変換を紹介した。前節のOrfanidisでも双一次変換を使っている。この変換は、s = 2 T 1 − z − 1 1 + z − 1 s=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}} s = T 2 1 + z − 1 1 − z − 1 s s s z z z s s s z z z s s s z z z
Matched Z-transform Method (MZT)は、アナログシステムの全ての極と零点を保ったままデジタルシステムに変換する方法である。具体的には、伝達関数が
H ( s ) = a M s M + ⋯ + a 1 s + a 0 b N s N + ⋯ + b 1 s + b 0 = a M b N ∏ i = 1 M ( s − ξ i ) ∏ i = 1 N ( s − p i ) \begin{aligned}
H(s) &= \frac{a_Ms^M+\cdots+a_1s+a_0}{b_Ns^N+\cdots+b_1s+b_0} \\
&= \frac{a_M}{b_N} \frac{\prod_{i=1}^M(s-\xi_i)}{\prod_{i=1}^N(s-p_i)}
\end{aligned} H ( s ) = b N s N + ⋯ + b 1 s + b 0 a M s M + ⋯ + a 1 s + a 0 = b N a M ∏ i = 1 N ( s − p i ) ∏ i = 1 M ( s − ξ i ) と書かれている時、零点ξ i \xi_i ξ i p i p_i p i T T T z = e s T z=e^{sT} z = e s T
H ( z ) = g a M b N ∏ i = 1 M ( z − e ξ i T ) ∏ i = 1 N ( z − e p i T ) H(z)=g\frac{a_M}{b_N}\frac{\prod_{i=1}^M(z-e^{\xi_iT})}{\prod_{i=1}^N(z-e^{p_iT})} H ( z ) = g b N a M ∏ i = 1 N ( z − e p i T ) ∏ i = 1 M ( z − e ξ i T ) とする。このように変形することで、元のアナログシステムが安定であれば、変換後のデジタルシステムも安定となる。なお、g g g H ( s ) H(s) H ( s ) H ( z ) H(z) H ( z )
なぜMZTiでは双一次変換ではなくMZTを用いるのか。それは、アナログフィルタとデジタルフィルタの特性の差分を考えたとき、MZTの方が差分の形が単純であり、補正が容易だからである。実際に見てみよう。Orfanidisでも扱ったピークフィルタを使う。中心周波数はω c \omega_c ω c
H ( s ) = ω c 2 − s 2 s 2 + 2 R ω c s + ω c 2 = − ( s − ω c ) ( s + ω c ) ( s + R ω c − ω c R 2 − 1 ) ( s + R ω c + ω c R 2 − 1 ) \begin{aligned}
H(s) &= \frac{\omega_c^2-s^2}{s^2+2R\omega_cs+\omega_c^2} \\
&= -\frac{(s-\omega_c)(s+\omega_c)}{(s+R\omega_c-\omega_c\sqrt{R^2-1})(s+R\omega_c+\omega_c\sqrt{R^2-1})}
\end{aligned} H ( s ) = s 2 + 2 R ω c s + ω c 2 ω c 2 − s 2 = − ( s + R ω c − ω c R 2 − 1 ) ( s + R ω c + ω c R 2 − 1 ) ( s − ω c ) ( s + ω c ) アナログシステムにおける零点は− ω c -\omega_c − ω c ω c \omega_c ω c − R ω c ± ω c R 2 − 1 -R\omega_c \plusmn \omega_c\sqrt{R^2-1} − R ω c ± ω c R 2 − 1 z = e s T z=e^{sT} z = e s T z z z
H ( z ) = − g ( z − e ω c T ) ( z − e − ω c T ) ( z − e ( − R ω c − ω c R 2 − 1 ) T ) ( z − e ( − R ω c + ω c R 2 − 1 ) T ) = g − z 2 + ( e ω c T + e − ω c T ) z − 1 z 2 − ( e ( − R ω c + ω c R 2 − 1 ) T + e ( − R ω c − ω c R 2 − 1 ) T ) z + e − 2 R ω c T = g − 1 + ( e ω c T + e − ω c T ) z − 1 − z − 2 1 − ( e ( − R ω c + ω c R 2 − 1 ) T + e ( − R ω c − ω c R 2 − 1 ) T ) z − 1 + e − 2 R ω c T z − 2 \begin{aligned}
H(z) &= -g\frac{(z-e^{\omega_cT})(z-e^{-\omega_cT})}{(z-e^{(-R\omega_c-\omega_c\sqrt{R^2-1})T})(z-e^{(-R\omega_c+\omega_c\sqrt{R^2-1})T})}\\
&= g\frac{-z^2+(e^{\omega_cT}+e^{-\omega_cT})z-1}{z^2-(e^{(-R\omega_c+\omega_c\sqrt{R^2-1})T}+e^{(-R\omega_c-\omega_c\sqrt{R^2-1})T})z + e^{-2R\omega_cT}} \\
&= g\frac{-1+(e^{\omega_cT}+e^{-\omega_cT})z^{-1}-z^{-2}}{1 - (e^{(-R\omega_c+\omega_c\sqrt{R^2-1})T}+e^{(-R\omega_c-\omega_c\sqrt{R^2-1})T})z^{-1} + e^{-2 R\omega_c T }z^{-2}
}
\end{aligned} H ( z ) = − g ( z − e ( − R ω c − ω c R 2 − 1 ) T ) ( z − e ( − R ω c + ω c R 2 − 1 ) T ) ( z − e ω c T ) ( z − e − ω c T ) = g z 2 − ( e ( − R ω c + ω c R 2 − 1 ) T + e ( − R ω c − ω c R 2 − 1 ) T ) z + e − 2 R ω c T − z 2 + ( e ω c T + e − ω c T ) z − 1 = g 1 − ( e ( − R ω c + ω c R 2 − 1 ) T + e ( − R ω c − ω c R 2 − 1 ) T ) z − 1 + e − 2 R ω c T z − 2 − 1 + ( e ω c T + e − ω c T ) z − 1 − z − 2 ここで、cosh x = e x + e − x 2 \cosh x = \frac{e^x+e^{-x}}{2} cosh x = 2 e x + e − x
H ( z ) = g − 1 + ( e ω c T + e − ω c T ) z − 1 − z − 2 1 − ( e ( − R ω c + ω c R 2 − 1 ) T + e ( − R ω c − ω c R 2 − 1 ) T ) z − 1 + e − 2 R ω c T z − 2 = g − 1 + ( 2 cosh ( ω c T ) ) z − 1 − z − 2 1 − ( 2 e − R ω c T cosh ( ω c T R 2 − 1 ) ) z − 1 + e − 2 R ω c T z − 2 \begin{aligned}
H(z) &= g\frac{-1+(e^{\omega_cT}+e^{-\omega_cT})z^{-1}-z^{-2}}{1 - (e^{(-R\omega_c+\omega_c\sqrt{R^2-1})T}+e^{(-R\omega_c-\omega_c\sqrt{R^2-1})T})z^{-1} + e^{-2 R\omega_c T }z^{-2}} \\
&= g\frac{-1+(2 \cosh(ω_cT))z^{-1}-z^{-2}}{1 - (2 e^{-R \omega_c T} \cosh( \omega_c T \sqrt{R^2 - 1}))z^{-1} + e^{-2 R\omega_c T }z^{-2}} \\
\end{aligned} H ( z ) = g 1 − ( e ( − R ω c + ω c R 2 − 1 ) T + e ( − R ω c − ω c R 2 − 1 ) T ) z − 1 + e − 2 R ω c T z − 2 − 1 + ( e ω c T + e − ω c T ) z − 1 − z − 2 = g 1 − ( 2 e − R ω c T cosh ( ω c T R 2 − 1 )) z − 1 + e − 2 R ω c T z − 2 − 1 + ( 2 cosh ( ω c T )) z − 1 − z − 2 最後にg g g H ( s ) H(s) H ( s ) s = 0 s=0 s = 0 H ( 0 ) = 1 H(0)=1 H ( 0 ) = 1 H ( z ) H(z) H ( z ) z = 1 z=1 z = 1
H ( 1 ) = g − 1 + ( 2 cosh ( ω c T ) ) − 1 1 − ( 2 e − R ω c T cosh ( ω c T R 2 − 1 ) ) + e − 2 R ω c T = g − 2 + 2 cosh ( ω c T ) 1 − ( 2 e − R ω c T cosh ( ω c T R 2 − 1 ) ) + e − 2 R ω c T = 1 \begin{aligned}
H(1)&=g\frac{-1+(2 \cosh(ω_cT))-1}{1 - (2 e^{-R \omega_c T} \cosh( \omega_c T \sqrt{R^2 - 1})) + e^{-2 R\omega_c T }}\\
&=g\frac{-2+2 \cosh(ω_cT)}{1 - (2 e^{-R \omega_c T} \cosh( \omega_c T \sqrt{R^2 - 1})) + e^{-2 R\omega_c T }}\\
&=1
\end{aligned} H ( 1 ) = g 1 − ( 2 e − R ω c T cosh ( ω c T R 2 − 1 )) + e − 2 R ω c T − 1 + ( 2 cosh ( ω c T )) − 1 = g 1 − ( 2 e − R ω c T cosh ( ω c T R 2 − 1 )) + e − 2 R ω c T − 2 + 2 cosh ( ω c T ) = 1 より、
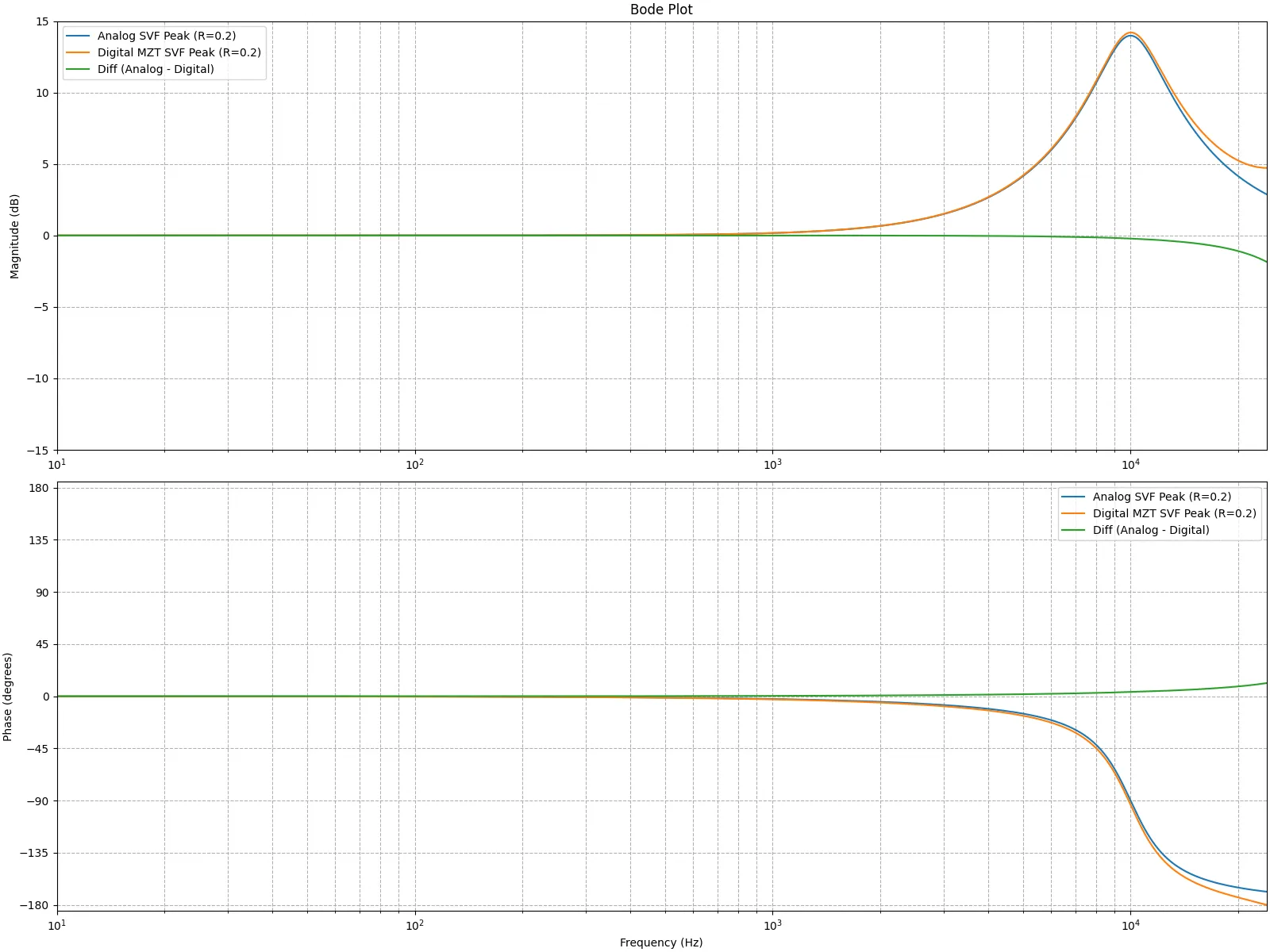
g = 1 − ( 2 e − R ω c T cosh ( ω c T R 2 − 1 ) ) + e − 2 R ω c T − 2 + 2 cosh ( ω c T ) g = \frac{1 - (2 e^{-R \omega_c T} \cosh( \omega_c T \sqrt{R^2 - 1})) + e^{-2 R\omega_c T }}{-2+2 \cosh(ω_cT)} g = − 2 + 2 cosh ( ω c T ) 1 − ( 2 e − R ω c T cosh ( ω c T R 2 − 1 )) + e − 2 R ω c T サンプリング周波数を48000Hz、中心周波数を10000Hz、R = 0.2 R=0.2 R = 0.2
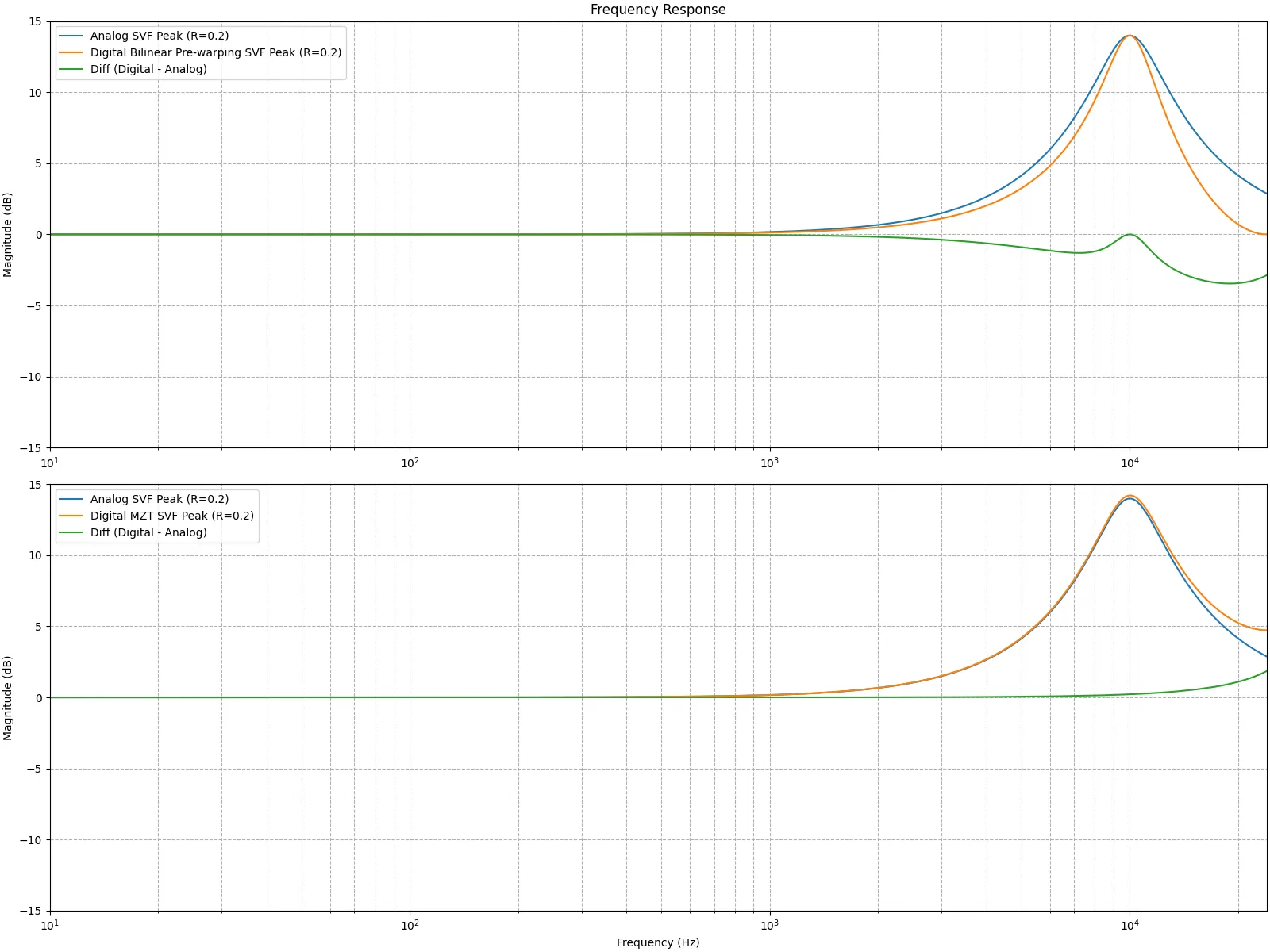
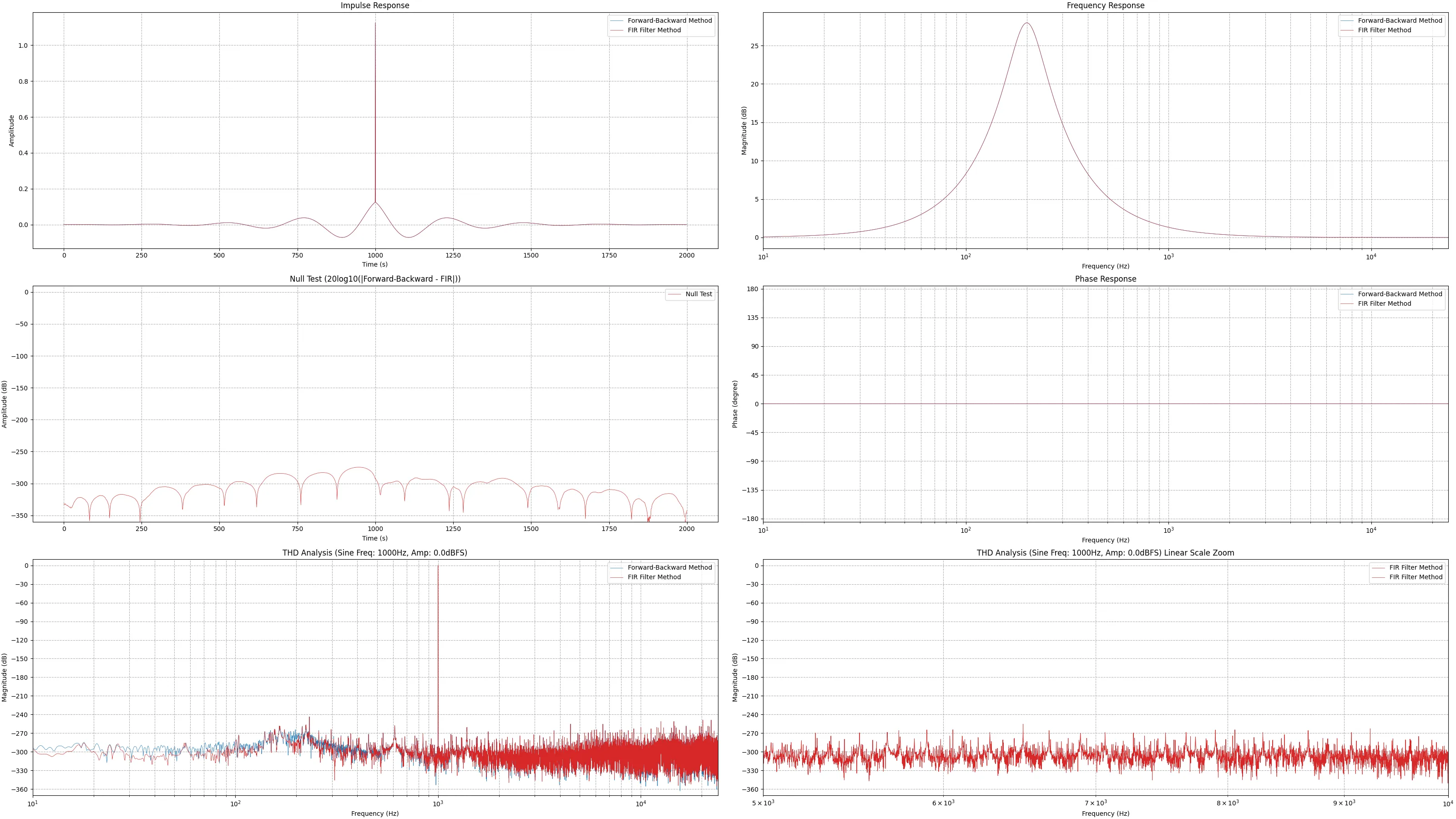
続いて、アナログフィルタの特性とデジタルフィルタの特性の差分をとって比較する。上段のグラフでは、双一次変換とプリワーピングで得たデジタルフィルタとアナログフィルタの振幅特性の差分を緑色のグラフで示している。下段のグラフでは、MZTで得たデジタルフィルタフィルタとアナログフィルタの差分を緑色のグラフで示している。デジタルフィルタに変換した後、何等かのフィルタを使って形状を補正する際、MZTの結果を補正したほうが簡単そうだと分かる。
補正フィルタの導出方法を示す。補正フィルタとしてFIRフィルタを用いる。元のアナログフィルタが2次である時、補正の対象となるMZTによるデジタルフィルタの周波数特性は
H D ( ω ) = g 1 + a 1 e − j ω T + a 2 e − 2 j ω T 1 + b 1 e − j ω T + b 2 e − 2 j ω T H_D(\omega) = g\frac{1+a_1e^{-j \omega T}+a_2e^{-2j \omega T}}{1+b_1e^{-j \omega T}+b_2e^{-2j \omega T}} H D ( ω ) = g 1 + b 1 e − jω T + b 2 e − 2 jω T 1 + a 1 e − jω T + a 2 e − 2 jω T である。一般に、FIRフィルタの伝達関数は
H F I R ( z ) = ∑ k = 0 M α k z − k H_{\mathit{FIR}}(z)=\sum_{k=0}^{M} \alpha_k z^{-k} H FIR ( z ) = k = 0 ∑ M α k z − k と表せるので、タップ数を決めて、いくつかの周波数でアナログフィルタの特性とMZT後のデジタルフィルタの特性が同じになるよう連立方程式をたてて、FIRフィルタの係数を求めれば良い。論文では、式を簡単にするため、ナイキスト周波数を等分するポイントで連立方程式を立式する方法を紹介している。
例えば、FIRフィルタの伝達関数がH F I R ( z ) = α 0 + α 1 z − 1 + α 2 z − 2 H_{\mathit{FIR}}(z)=\alpha_0+\alpha_1z^{-1}+\alpha_2z^{-2} H FIR ( z ) = α 0 + α 1 z − 1 + α 2 z − 2
∣ H D ( f N / 3 ) ∣ = g 1 + a 1 − a 2 + a 1 2 + a 1 a 2 + a 2 2 1 + b 1 − b 2 + b 1 2 + b 1 b 2 + b 2 2 ∣ H D ( 2 f N / 3 ) ∣ = g 1 − a 1 − a 2 + a 1 2 − a 1 a 2 + a 2 2 1 − b 1 − b 2 + b 1 2 − b 1 b 2 + b 2 2 \begin{aligned}
|H_D(f_N / 3)| &= g \frac{\sqrt{1 + a_1 - a_2 + a_1^2 + a_1 a_2 + a_2^2}}{\sqrt{1 + b_1 - b_2 + b_1^2 + b_1 b_2 + b_2^2}} \\
|H_D(2f_N / 3)| &= g \frac{\sqrt{1 - a_1 - a_2 + a_1^2 - a_1 a_2 + a_2^2}}{\sqrt{1 - b_1 - b_2 + b_1^2 - b_1 b_2 + b_2^2}}
\end{aligned} ∣ H D ( f N /3 ) ∣ ∣ H D ( 2 f N /3 ) ∣ = g 1 + b 1 − b 2 + b 1 2 + b 1 b 2 + b 2 2 1 + a 1 − a 2 + a 1 2 + a 1 a 2 + a 2 2 = g 1 − b 1 − b 2 + b 1 2 − b 1 b 2 + b 2 2 1 − a 1 − a 2 + a 1 2 − a 1 a 2 + a 2 2 であり、同地点の補正FIRフィルタの周波数特性をH 1 H_1 H 1 H 2 H_2 H 2 H 0 H_0 H 0
α 0 = H 0 − α 1 − α 2 α 1 = H 0 − H 0 2 − 2 H 1 2 + 2 H 2 2 2 α 2 = 3 ( H 0 − α 1 ) − − 3 H 0 2 + 12 H 1 2 − 6 H 0 α 1 − 3 α 1 2 6 \begin{aligned}
\alpha_0 &= H_0 - \alpha_1 - \alpha_2\\
\alpha_1 &= \frac{H_0 - \sqrt{H_0^2 - 2H_1^2 + 2H_2^2}}{2}\\
\alpha_2 &= \frac{3(H_0 - \alpha_1) - \sqrt{-3H_0^2 + 12H_1^2 - 6H_0 \alpha_1 - 3\alpha_1^2}}{6}
\end{aligned} α 0 α 1 α 2 = H 0 − α 1 − α 2 = 2 H 0 − H 0 2 − 2 H 1 2 + 2 H 2 2 = 6 3 ( H 0 − α 1 ) − − 3 H 0 2 + 12 H 1 2 − 6 H 0 α 1 − 3 α 1 2 この補正FIRフィルタを、MZT後のデジタルフィルタの後に掛けることで、DC成分・ナイキスト周波数の3分の1の地点・ナイキスト周波数の3分の2の地点の振幅特性がアナログフィルタの特性と一致するフィルタを得ることができる。
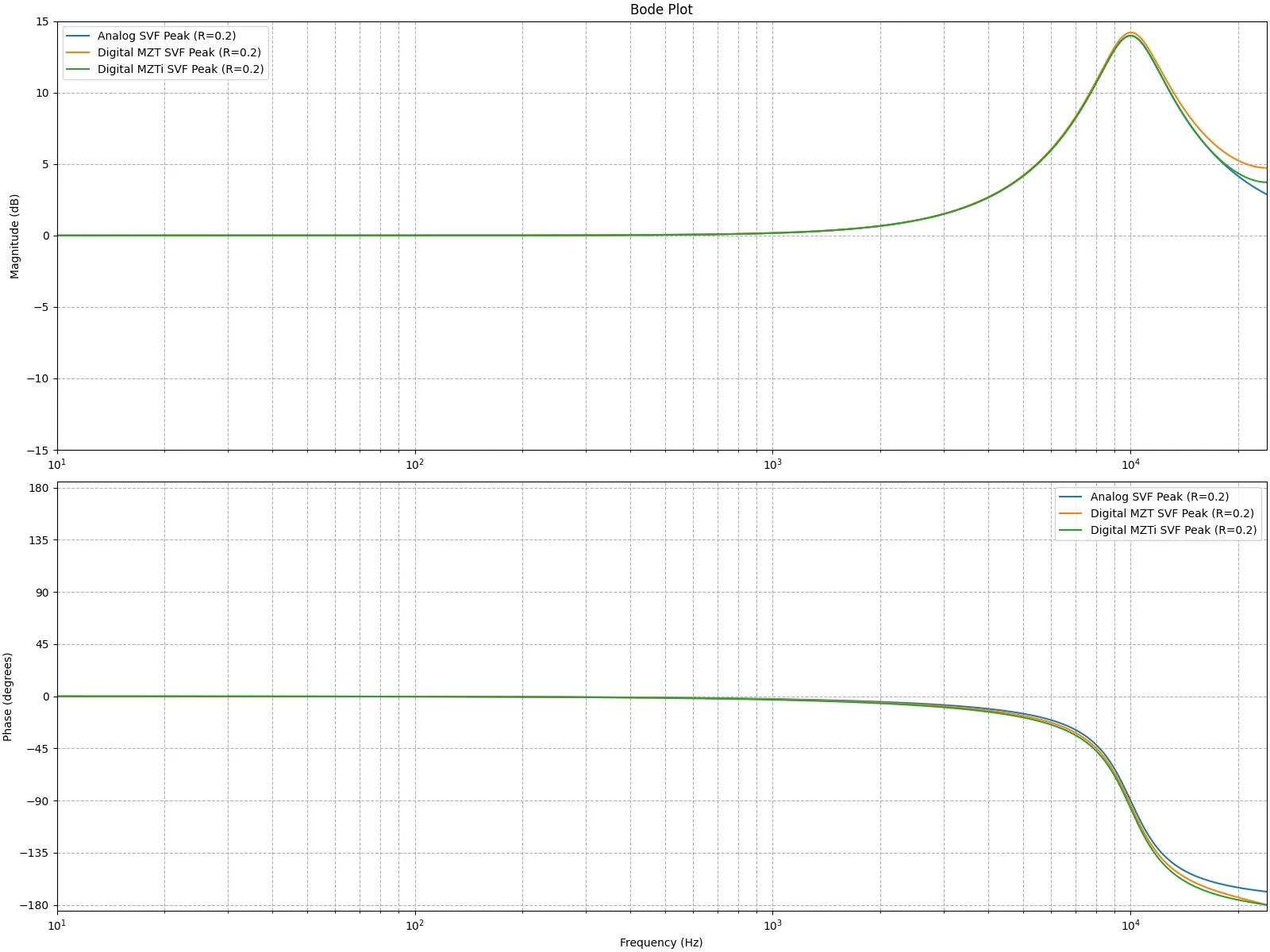
サンプリング周波数を48000Hz、中心周波数を10000Hz、R = 0.2 R=0.2 R = 0.2
その他の著名な方法(Balance Mastering Magpha EQ / DDMF GrandEQ / Kush Audio q.632)
J. Flynn and J. D. Reiss, “Improving the frequency response magnitude and phase of analogue-matched digital filters,” Journal of the Audio Engineering Society, May 2018.
MZTiはかなり優秀な手法である。MZTiで得たデジタルフィルタの特性はアナログフィルタにかなり近い。が、完璧に一致してはいない。
MZTiを改善しようと試みる時、補正FIRフィルタの算出方法を改善すれば良いのでは?と思うのはとても自然である。MZTiの補正フィルタは、ナイキスト周波数未満を等分した数点の振幅特性がアナログフィルタの振幅特性に一致するよう、連立方程式をたててFIRフィルタの係数を求めている。そうではなく、MZT後のデジタルフィルタの特性とアナログフィルタの特性の差を逆フーリエ変換してFIRフィルタの係数を求めた方が、よりアナログフィルタの特性を近似できるだろうというのは直感的に理解できる。
この改善案を採用したのが、これから紹介する手法である。
これはただの感想ですが…。
既に述べたように、MZTiを知っていれば、この改善案は割と誰でも思いつくレベルだと思います。
そしてMZTiはそれほどマイナーな手法ではありません(Wikipediaにも載ってるレベル)。
なので、Magpha EQ/GrandEQ/q.632以外で、これと似たような方法を実装したEQは数多く存在すると思います。
MZTiの項で述べたように、元のアナログフィルタの伝達関数が
H A ( s ) = a M s M + ⋯ + a 1 s + a 0 b N s N + ⋯ + b 1 s + b 0 = a M b N ∏ i = 1 M ( s − ξ i ) ∏ i = 1 N ( s − p i ) \begin{aligned}
H_A(s) &= \frac{a_Ms^M+\cdots+a_1s+a_0}{b_Ns^N+\cdots+b_1s+b_0} \\
&= \frac{a_M}{b_N} \frac{\prod_{i=1}^M(s-\xi_i)}{\prod_{i=1}^N(s-p_i)}
\end{aligned} H A ( s ) = b N s N + ⋯ + b 1 s + b 0 a M s M + ⋯ + a 1 s + a 0 = b N a M ∏ i = 1 N ( s − p i ) ∏ i = 1 M ( s − ξ i ) と書かれている時、全ての零点ξ i \xi_i ξ i p i p_i p i T T T z = e s T z=e^{sT} z = e s T
H M Z T ( z ) = g a M b N ∏ i = 1 M ( z − e ξ i T ) ∏ i = 1 N ( z − e p i T ) H_{\mathit{MZT}}(z)=g\frac{a_M}{b_N}\frac{\prod_{i=1}^M(z-e^{\xi_iT})}{\prod_{i=1}^N(z-e^{p_iT})} H MZT ( z ) = g b N a M ∏ i = 1 N ( z − e p i T ) ∏ i = 1 M ( z − e ξ i T ) である。
アナログフィルタの周波数特性はs = j ω s=j\omega s = jω
H A ( j ω ) = a M b N ∏ i = 1 M ( j ω − ξ i ) ∏ i = 1 N ( j ω − p i ) \begin{aligned}
H_A(j\omega) = \frac{a_M}{b_N} \frac{\prod_{i=1}^M(j\omega-\xi_i)}{\prod_{i=1}^N(j\omega-p_i)}
\end{aligned} H A ( jω ) = b N a M ∏ i = 1 N ( jω − p i ) ∏ i = 1 M ( jω − ξ i ) デジタルフィルタの周波数特性はz = e j ω z=e^{j\omega} z = e jω
H M Z T ( e j ω ) = g a M b N ∏ i = 1 M ( e j ω − e ξ i T ) ∏ i = 1 N ( e j ω − e p i T ) H_{\mathit{MZT}}(e^{j\omega})=g\frac{a_M}{b_N}\frac{\prod_{i=1}^M(e^{j\omega}-e^{\xi_iT})}{\prod_{i=1}^N(e^{j\omega}-e^{p_iT})} H MZT ( e jω ) = g b N a M ∏ i = 1 N ( e jω − e p i T ) ∏ i = 1 M ( e jω − e ξ i T ) これら周波数特性の差は、応答の比で表すと
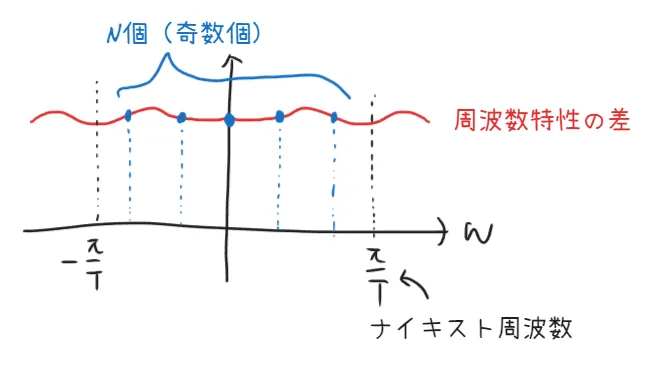
H d i f f ( ω ) = H A ( j ω ) H M Z T ( e j ω ) H_{\mathrm{diff}}(\omega) = \frac{H_A(j\omega)}{H_{\mathit{MZT}}(e^{j\omega})} H diff ( ω ) = H MZT ( e jω ) H A ( jω ) この応答の比からサンプル点をN N N T T T π T \frac{\pi}{T} T π N N N ω n \omega_n ω n
ω n = π T N / 2 × n = 2 π n N T , n = − N − 1 2 , ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ , N − 1 2 \omega_n = \frac{\frac{\pi}{T}}{N/2}\times n=\frac{2 \pi n}{NT}, \quad n=-\frac{N-1}{2}, \cdots,-2,-1,0,1,2,\cdots,\frac{N-1}{2} ω n = N /2 T π × n = NT 2 πn , n = − 2 N − 1 , ⋯ , − 2 , − 1 , 0 , 1 , 2 , ⋯ , 2 N − 1
これを代入したH d i f f ( ω n ) に H_{\mathrm{diff}}(\omega_n)に H diff ( ω n ) に H d i f f ( z ) H_{\mathrm{diff}}(z) H diff ( z )
最終的に、
H D ( z ) = H M Z T ( z ) ⋅ H d i f f ( z ) H_D(z)=H_{\mathit{MZT}}(z) \cdot H_{\mathrm{diff}}(z) H D ( z ) = H MZT ( z ) ⋅ H diff ( z ) で、所望のデジタルフィルタを得る。
実際に作って見よう。MZTiでも扱ったピークフィルタを題材とする。
H A ( s ) = ω c 2 − s 2 s 2 + 2 R ω c s + ω c 2 = − ( s − ω c ) ( s + ω c ) ( s + R ω c − ω c R 2 − 1 ) ( s + R ω c + ω c R 2 − 1 ) \begin{aligned}
H_A(s) &= \frac{\omega_c^2-s^2}{s^2+2R\omega_cs+\omega_c^2} \\
&= -\frac{(s-\omega_c)(s+\omega_c)}{(s+R\omega_c-\omega_c\sqrt{R^2-1})(s+R\omega_c+\omega_c\sqrt{R^2-1})}
\end{aligned} H A ( s ) = s 2 + 2 R ω c s + ω c 2 ω c 2 − s 2 = − ( s + R ω c − ω c R 2 − 1 ) ( s + R ω c + ω c R 2 − 1 ) ( s − ω c ) ( s + ω c ) MZTして、
H M Z T ( z ) = − g ( z − e ω c T ) ( z − e − ω c T ) ( z − e ( − R ω c − ω c R 2 − 1 ) T ) ( z − e ( − R ω c + ω c R 2 − 1 ) T ) = g − 1 + ( e ω c T + e − ω c T ) z − 1 − z − 2 1 − ( e ( − R ω c + ω c R 2 − 1 ) T + e ( − R ω c − ω c R 2 − 1 ) T ) z − 1 + e − 2 R ω c T z − 2 \begin{aligned}
H_{\mathit{MZT}}(z) &= -g\frac{(z-e^{\omega_cT})(z-e^{-\omega_cT})}{(z-e^{(-R\omega_c-\omega_c\sqrt{R^2-1})T})(z-e^{(-R\omega_c+\omega_c\sqrt{R^2-1})T})}\\
&= g\frac{-1+(e^{\omega_cT}+e^{-\omega_cT})z^{-1}-z^{-2}}{1 - (e^{(-R\omega_c+\omega_c\sqrt{R^2-1})T}+e^{(-R\omega_c-\omega_c\sqrt{R^2-1})T})z^{-1} + e^{-2 R\omega_c T }z^{-2}}
\end{aligned} H MZT ( z ) = − g ( z − e ( − R ω c − ω c R 2 − 1 ) T ) ( z − e ( − R ω c + ω c R 2 − 1 ) T ) ( z − e ω c T ) ( z − e − ω c T ) = g 1 − ( e ( − R ω c + ω c R 2 − 1 ) T + e ( − R ω c − ω c R 2 − 1 ) T ) z − 1 + e − 2 R ω c T z − 2 − 1 + ( e ω c T + e − ω c T ) z − 1 − z − 2 そしてg g g
g = 1 − ( 2 e − R ω c T cosh ( ω c T R 2 − 1 ) ) + e − 2 R ω c T − 2 + 2 cosh ( ω c T ) g = \frac{1 - (2 e^{-R \omega_c T} \cosh( \omega_c T \sqrt{R^2 - 1})) + e^{-2 R\omega_c T }}{-2+2 \cosh(ω_cT)} g = − 2 + 2 cosh ( ω c T ) 1 − ( 2 e − R ω c T cosh ( ω c T R 2 − 1 )) + e − 2 R ω c T H A ( s ) H_A(s) H A ( s ) H M Z T ( z ) H_{\mathit{MZT}}(z) H MZT ( z )
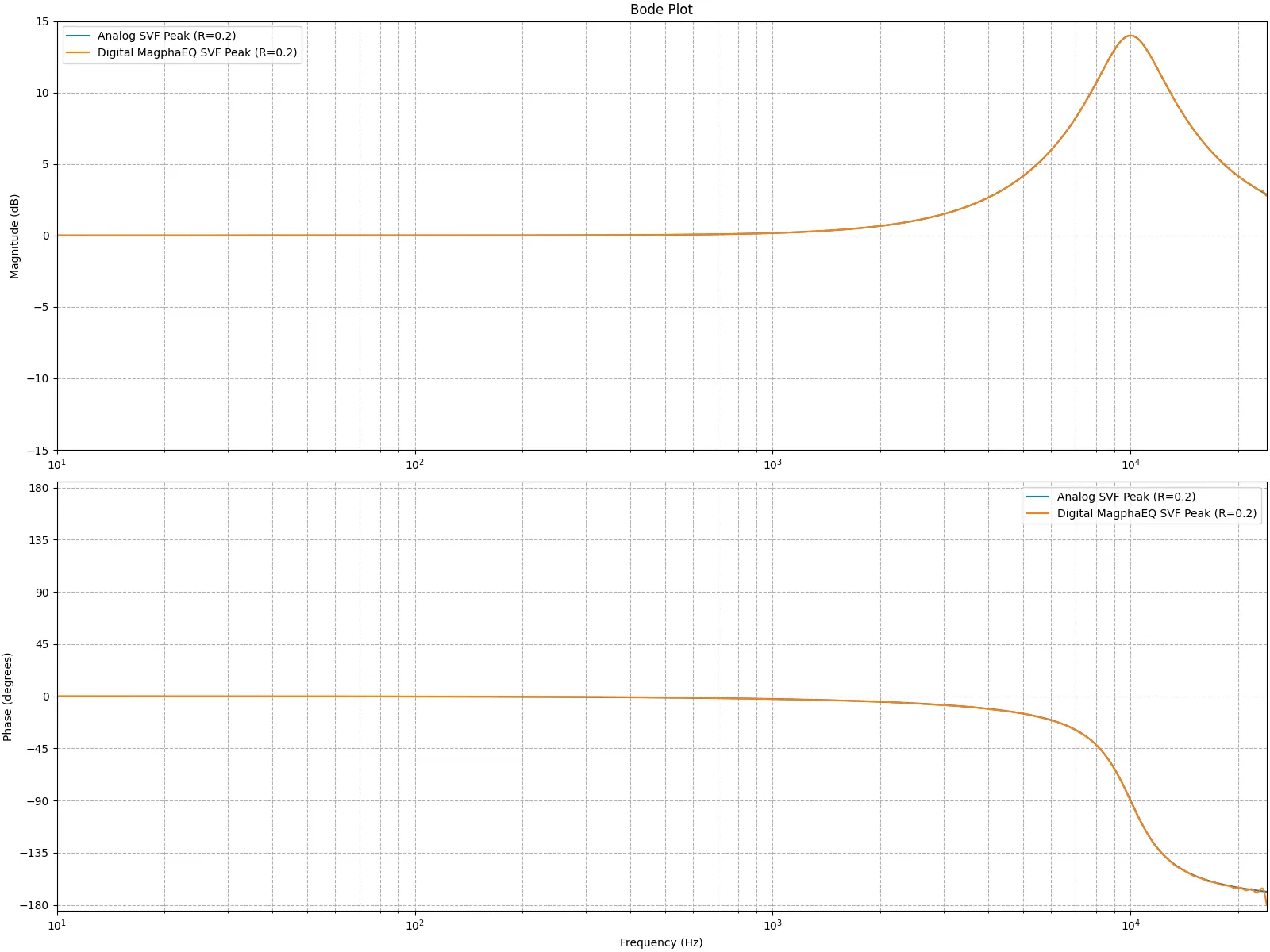
H d i f f ( ω ) = H A ( j ω ) H M Z T ( e j ω ) H_{\mathrm{diff}}(\omega) = \frac{H_A(j\omega)}{H_{\mathit{MZT}}(e^{j\omega})} H diff ( ω ) = H MZT ( e jω ) H A ( jω ) サンプリング周波数を48000Hz、中心周波数を10000Hz、R = 0.2 R=0.2 R = 0.2 H A ( s ) H_A(s) H A ( s ) H M Z T ( z ) H_{\mathit{MZT}(z)} H MZT ( z ) H d i f f ( ω ) H_{\mathrm{diff}}(\omega) H diff ( ω ) H d i f f ( ω ) H_{\mathrm{diff}}(\omega) H diff ( ω )
(※MZTiで紹介したグラフと緑色のグラフの形が違うが、MZTiの項ではDigital - Analogを描画し、ここではAnalog - Digitalを描画しているからである。)
ここから先はグラフを用いながら説明する。
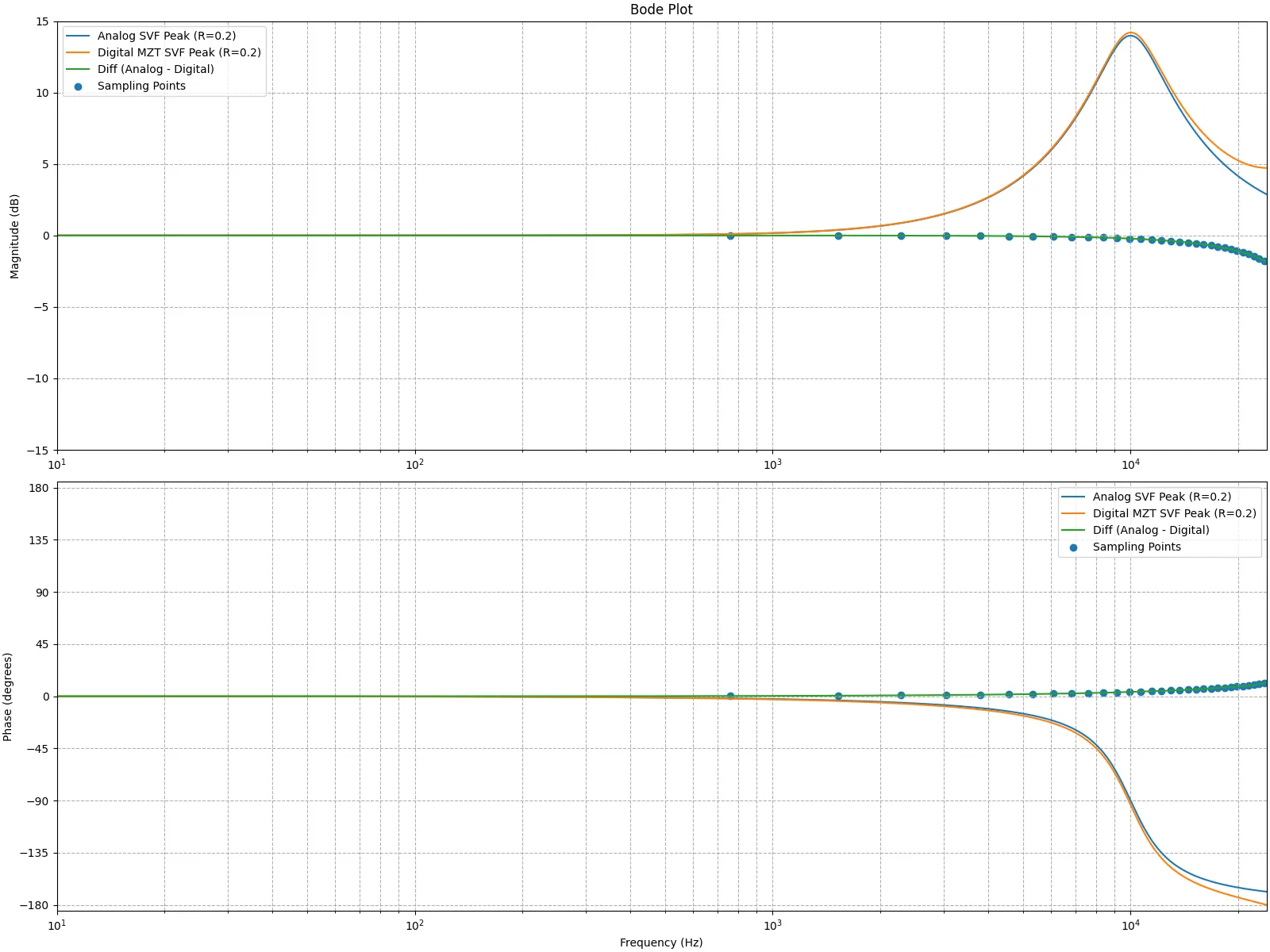
周波数サンプル点の個数をN = 63 N=63 N = 63 H d i f f ( ω ) H_{\mathrm{diff}}(\omega) H diff ( ω ) N N N
このサンプル点を逆離散フーリエ変換することで、補正FIRフィルタH d i f f ( z ) H_{\mathrm{diff}}(z) H diff ( z )
最後にH D ( z ) = H M Z T ( z ) ⋅ H d i f f ( z ) H_D(z)=H_{\mathit{MZT}}(z) \cdot H_{\mathrm{diff}}(z) H D ( z ) = H MZT ( z ) ⋅ H diff ( z )
ちょっと乱暴な方法(双一次変換+オーバーサンプリング)
これまで色々試行錯誤を重ね、アナログフィルタの特性をデジタルフィルタに落とし込んできた。どの手法も、ナイキスト周波数付近で生じる特性の歪みを抑えようと工夫を凝らしてきた。しかし、オーバーサンプリングを行い、ナイキスト周波数を可聴域の外に移せば、特性の歪みも可聴域外に押し出される。そうすれば、アナログフィルタの特性により近いデジタルフィルタを、もっと簡単に実現できるのではないだろうか。
これは、正しい。双一次変換による特性の歪は、アナログフィルタの周波数をΩ \Omega Ω ω \omega ω
Ω = 2 T tan ω T 2 \begin{aligned}
\Omega &= \frac{2}{T} \tan \frac{\omega T}{2}
\end{aligned} Ω = T 2 tan 2 ω T と書けるのは前に扱った。このグラフを、異なるサンプリング周波数で描画してみよう。横軸と縦軸は10Hzから24000Hzの範囲を描画している。
このグラフから、双一次変換しただけの教科書的な実装のEQでも、サンプリング周波数が192kHzや384kHzであればほぼ理想的な関係Ω = ω \Omega=\omega Ω = ω
直前に扱ったMagpha EQの手法でも、サンプリング周波数を上げれば補正フィルタが掛かり始める帯域が上方向にずれていく。その結果、ほんのごく僅かながらもフィルタの形状が変わったり、数値演算上の誤差が変わって、音が理論上変わることはあり得る(知覚できるかどうかは置いておいて…)。
普通、「サンプリング周波数を変えたりオーバーサンプリングしたら音が変わった」系の話は、コンプレッサやサチュレータなど非線形歪みを発生させる処理や、エイリアシングフィルタのスペックが違うからという説明で語られることが多い。しかし、ここで話したように、非線形歪みを発生させないEQでも、音が変わることは全然ありえるという事実は頭の片隅に置いておくべきである。
Chapter 3. IIRデジタルフィルタの実装
Chapter 2.では、主にアナログフィルタの伝達関数H ( s ) H(s) H ( s ) H ( z ) H(z) H ( z ) H ( z ) H(z) H ( z )
H ( z ) = Y ( z ) X ( z ) = ∑ k = 0 M a k z − k 1 + ∑ k = 1 N b k z − k H(z)=\frac{Y(z)}{X(z)} = \frac{\sum_{k=0}^{M} a_k z^{-k}}{1+\sum_{k=1}^{N} b_k z^{-k}} H ( z ) = X ( z ) Y ( z ) = 1 + ∑ k = 1 N b k z − k ∑ k = 0 M a k z − k のように、有理関数で表すことができる。このように表せたら、差分方程式
y ( n T ) = a 0 x ( n T ) + a 1 x ( n T − T ) + ⋯ + a M x ( n T − M T ) − ( b 0 y ( n T ) + b 1 y ( n T − T ) + ⋯ + b M y ( n T − N T ) ) = ∑ k = 0 M a k x ( n T − k T ) − ∑ k = 1 N b k y ( n T − k T ) \begin{aligned}
y(nT) &= a_0x(nT) + a_1x(nT-T) + \cdots + a_Mx(nT-MT) \\
& \qquad -(b_0y(nT) + b_1y(nT-T) + \cdots + b_My(nT-NT)) \\
&= \sum_{k=0}^{M} a_k x(nT-kT) - \sum_{k=1}^{N}b_ky(nT-kT) \\
\end{aligned} y ( n T ) = a 0 x ( n T ) + a 1 x ( n T − T ) + ⋯ + a M x ( n T − MT ) − ( b 0 y ( n T ) + b 1 y ( n T − T ) + ⋯ + b M y ( n T − NT )) = k = 0 ∑ M a k x ( n T − k T ) − k = 1 ∑ N b k y ( n T − k T ) を計算すれば、入力信号から出力信号を得ることができる。
つまり、これをプログラムで実装すればIIRデジタルフィルタの実装が完了するのだが、実はそう上手くは行かない。何故なら、コンピュータの世界では数値は有限桁数であり、計算には少なからず誤差が生じるからである。極端な場合その誤差が積み重なって、理論上安定なフィルタが不安定になることもあり得る。この章では、浮動小数点演算の誤差について説明した後、計算をブロックダイアグラムで図示するブロック法をまとめ、様々なデジタルフィルタの計算方法をブロックダイアグラムで示し、誤差を抑えたデジタルフィルタの計算方法を実験により調べる。
コンピュータの世界の数値表現(浮動小数点数)と演算誤差
コンピュータは2進数(0と1)で数値を表現する。例えば、10進数における10 10 10 1010と表現される。コンピュータでは桁数を固定してメモリに値を格納することが多い。この桁数のことをbit幅と呼ぶ。例えば、44.1kHz/16bitで記録されたCD音質のWAVファイルは、1サンプルの振幅を16bitのbit幅、つまり16桁の0と1で表現している。10進数で10 10 10 0000 0000 0000 1010となる(注1)。
次に小数の表現方法について紹介する。小数の表現には固定小数点と浮動小数点の2種類がある。
固定小数点は、小数点の位置を予め決めておく方法である。例えば、2進数で下位5bitは小数点以下の数字を表す…といった感じである。現代のパソコンでは浮動小数点で小数を扱うことが多い。
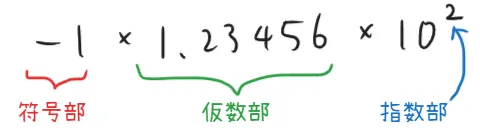
浮動小数点は、数を符号部・固定長の指数部・固定長の仮数部で表す方法である。10進数で例えるなら、− 123.456 -123.456 − 123.456 − 1 × 1.23456 × 10 2 -1\times1.23456\times10^{2} − 1 × 1.23456 × 1 0 2
標準規格IEEE 754に則れば、32bit浮動小数点は符号部1bit・指数部8bit・仮数部23bitである。仮数部は、整数部分が1であるような2進小数の小数部分を示す。つまり、2進数で1010と表せる値を32bit浮動小数点で表現するなら、仮数部は先頭の1を除いて010となる。実質的に仮数部は24bitなので、32bit浮動小数点の10進数における有効桁数は24 × log 10 2 ≈ 7 24\times\log_{10}2 \approx 7 24 × log 10 2 ≈ 7
64bit浮動小数点は符号部1bit・指数部11bit・仮数部52bitである。10進数における有効桁数は53 × log 10 2 ≈ 16 53\times\log_{10}2 \approx 16 53 × log 10 2 ≈ 16
これから、浮動小数点演算で生じる代表的な演算誤差について、いくつか紹介する。
丸め誤差
浮動小数点数は有限桁の仮数部を持つため、無限に続く循環小数を正確に表現することはできない。例えば、10進数における0.1 0.1 0.1 0.00011001100110011001100 ⋯ 0.00011001100110011001100\cdots 0.00011001100110011001100 ⋯
実際、0.1を32bit浮動小数点(float型)、64bit浮動小数点(double型)で定義して10進数で表示させると、
std ::cout << std :: setprecision ( 200 ) << 0.1 f << std ::endl; // -> 0.100000001490116119384765625 std ::cout << std :: setprecision ( 200 ) << 0.1 << std ::endl; // -> 0.1000000000000000055511151231257827021181583404541015625 となり、どちらも0.1ではないことが分かる。これが及ぼす悪影響を見てみよう。
今、float型の0.1を1000回加算するプログラムを書いた。結果は100になるはずだが、実際はそうなっていない。
int main () { float x = 0.0 ; for ( int i = 0 ; i < 1000 ; i ++ ) { x += 0.1 f ; } std ::cout << std :: setprecision ( 200 ) << x << std ::endl; // -> 99.99904632568359375 return 0 ; } double型でも100にならない。
int main () { double x = 0.0 ; for ( int i = 0 ; i < 1000 ; i ++ ) { x += 0.1 ; } std ::cout << std :: setprecision ( 200 ) << x << std ::endl; // -> 99.9999999999985931253831950016319751739501953125 return 0 ; } 情報落ち
a + b a+b a + b a a a b b b 12345600 + 1 = 12345601 12345600+1=12345601 12345600 + 1 = 12345601 1.23456 × 10 7 + 1.00000 = 1.2345601 × 10 7 ≈ 1.23456 × 10 7 1.23456\times10^{7}+1.00000=1.2345601\times10^{7}\approx1.23456\times10^{7} 1.23456 × 1 0 7 + 1.00000 = 1.2345601 × 1 0 7 ≈ 1.23456 × 1 0 7
下記のプログラムでは100000000に1を1000回加算しているが、結果は100000000のままである。
int main () { float x = 100000000.0 ; for ( int i = 0 ; i < 1000 ; i ++ ) { x += 1.0 ; } std ::cout << std :: setprecision ( 200 ) << x << std ::endl; // -> 100000000 return 0 ; } 桁落ち
a − b a-b a − b a a a b b b
下記のプログラムでは、1.000001 − 1.0 = 0.000001 = 1 × 10 − 6 1.000001-1.0=0.000001=1\times10^{-6} 1.000001 − 1.0 = 0.000001 = 1 × 1 0 − 6
int main () { float a = 1.000001 ; float b = 1.0 ; float x = a - b; std ::cout << std :: setprecision ( 200 ) << x << std ::endl; // -> 9.5367431640625e-07 return 0 ; } 注1
簡単の為に説明を省略したが、WAVファイルにおけるint16(符号付き整数型)の内部表現はもう少し複雑である。10を表現するなら本当に0000 0000 0000 1010だが、-10を表現する場合は2の補数表現を用いて2 16 − 10 2^{16}-10 2 16 − 10 1111 1111 1111 0110である。ちなみに、プログラムにおけるint16およびint型の内部表現は処理系依存で、負値の表し方は2の補数表現・1の補数表現・符号bitと絶対値、のいずれかである。
ブロック法
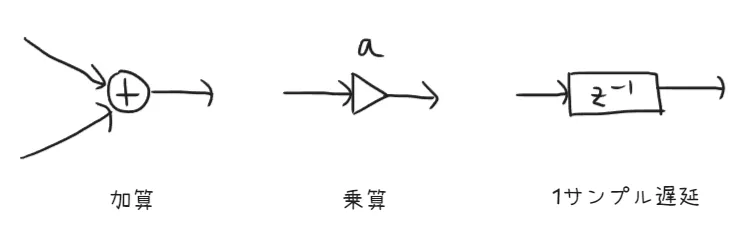
この次にデジタルフィルタの計算方法をいくつか紹介したいが、式で表すと直感的でないことがある。そこで、計算の流れをブロックダイアグラムで示す「ブロック法」をまず紹介する。
デジタルフィルタの実現に必要な演算は加算・乗算・1サンプル遅延の3つであり、それぞれブロックで表すと次のようになる。
そして、これらブロックからなる1塊の回路を単位ブロックとみなして、それらの組み合わせを考える。単位ブロックの伝達関数をF F F G G G
縦続接続
伝達関数を考えれば、
X 1 X i n = F , X o u t X 1 = G \frac{X_1}{X_{\mathrm{in}}} = F, \quad \frac{X_{\mathrm{out}}}{X_1} = G X in X 1 = F , X 1 X out = G なので、
X o u t X i n = F G \frac{X_{\mathrm{out}}}{X_{\mathrm{in}}}=FG X in X out = FG 並列接続
X o u t = X 1 + X 2 = F X i n + G X i n X_{\mathrm{out}}=X_1+X_2=FX_{\mathrm{in}}+GX_{\mathrm{in}} X out = X 1 + X 2 = F X in + G X in
X o u t X i n = F + G \frac{X_{\mathrm{out}}}{X_{\mathrm{in}}}=F+G X in X out = F + G 帰還接続
関係式を立てると、
X 1 = X i n − X 2 , X o u t = X 1 F , X 2 = G X o u t X_1=X_{\mathrm{in}}-X_2, \quad X_{\mathrm{out}}=X_1F, \quad X_2=GX_{\mathrm{out}} X 1 = X in − X 2 , X out = X 1 F , X 2 = G X out ここからX 1 X_1 X 1 X 2 X_2 X 2
X o u t = F ( X i n − G X o u t ) X_{\mathrm{out}}=F(X_{\mathrm{in}}-GX_{\mathrm{out}}) X out = F ( X in − G X out ) これを整理すれば
X o u t X i n = F 1 + F G \frac{X_{\mathrm{out}}}{X_{\mathrm{in}}}=\frac{F}{1+FG} X in X out = 1 + FG F デジタルフィルタの計算方法はブロックダイアグラムで表すことができることから、デジタルフィルタの回路と言ったり、デジタルフィルタのトポロジと言ったりする。
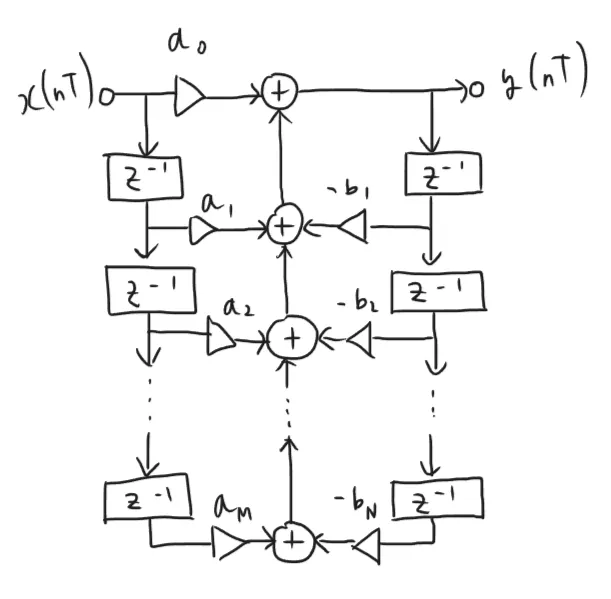
前提知識の章で、離散時間システムの入出力関係の式は差分方程式を用いて
y ( n T ) = a 0 x ( n T ) + a 1 x ( n T − T ) + ⋯ + a M x ( n T − M T ) − ( b 0 y ( n T ) + b 1 y ( n T − T ) + ⋯ + b M y ( n T − N T ) ) = ∑ k = 0 M a k x ( n T − k T ) − ∑ k = 1 N b k y ( n T − k T ) \begin{aligned}
y(nT) &= a_0x(nT) + a_1x(nT-T) + \cdots + a_Mx(nT-MT) \\
& \qquad -(b_0y(nT) + b_1y(nT-T) + \cdots + b_My(nT-NT)) \\
&= \sum_{k=0}^{M} a_k x(nT-kT) - \sum_{k=1}^{N}b_ky(nT-kT) \\
\end{aligned} y ( n T ) = a 0 x ( n T ) + a 1 x ( n T − T ) + ⋯ + a M x ( n T − MT ) − ( b 0 y ( n T ) + b 1 y ( n T − T ) + ⋯ + b M y ( n T − NT )) = k = 0 ∑ M a k x ( n T − k T ) − k = 1 ∑ N b k y ( n T − k T ) で表現でき、これの両辺をZ変換して変形を行い、
Y ( z ) = ∑ k = 0 M a k z − k X ( Z ) − ∑ k = 1 N b k z − k Y ( z ) Y ( z ) X ( z ) = ∑ k = 0 M a k z − k 1 + ∑ k = 1 N b k z − k \begin{aligned}
Y(z) &= \sum_{k=0}^{M} a_k z^{-k} X(Z) - \sum_{k=1}^{N} b_k z^{-k}Y(z) \\
\frac{Y(z)}{X(z)} &= \frac{\sum_{k=0}^{M} a_k z^{-k}}{1+\sum_{k=1}^{N} b_k z^{-k}}
\end{aligned} Y ( z ) X ( z ) Y ( z ) = k = 0 ∑ M a k z − k X ( Z ) − k = 1 ∑ N b k z − k Y ( z ) = 1 + ∑ k = 1 N b k z − k ∑ k = 0 M a k z − k とした物が離散時間システムの伝達関数H ( z ) H(z) H ( z ) H ( z ) H(z) H ( z )
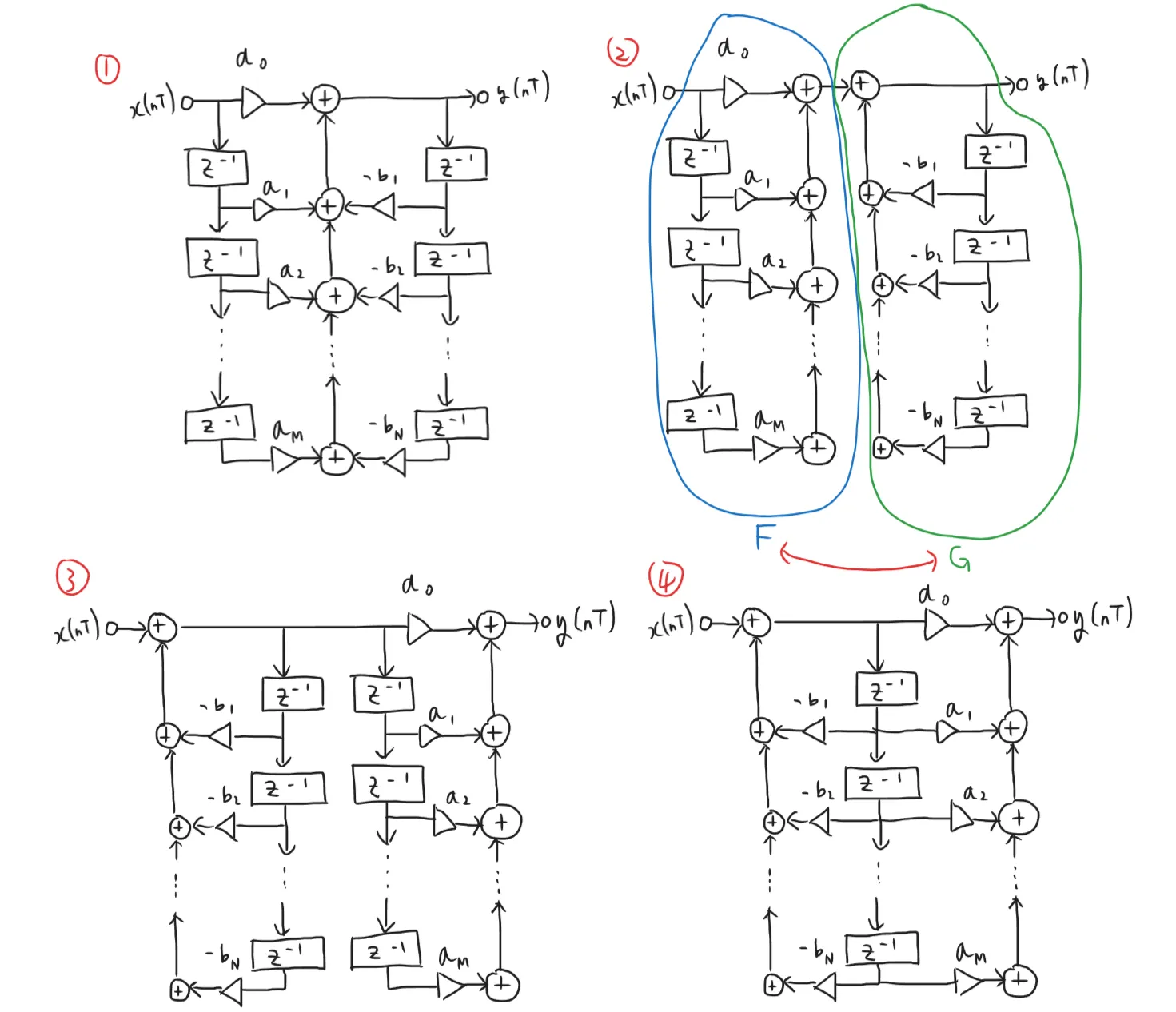
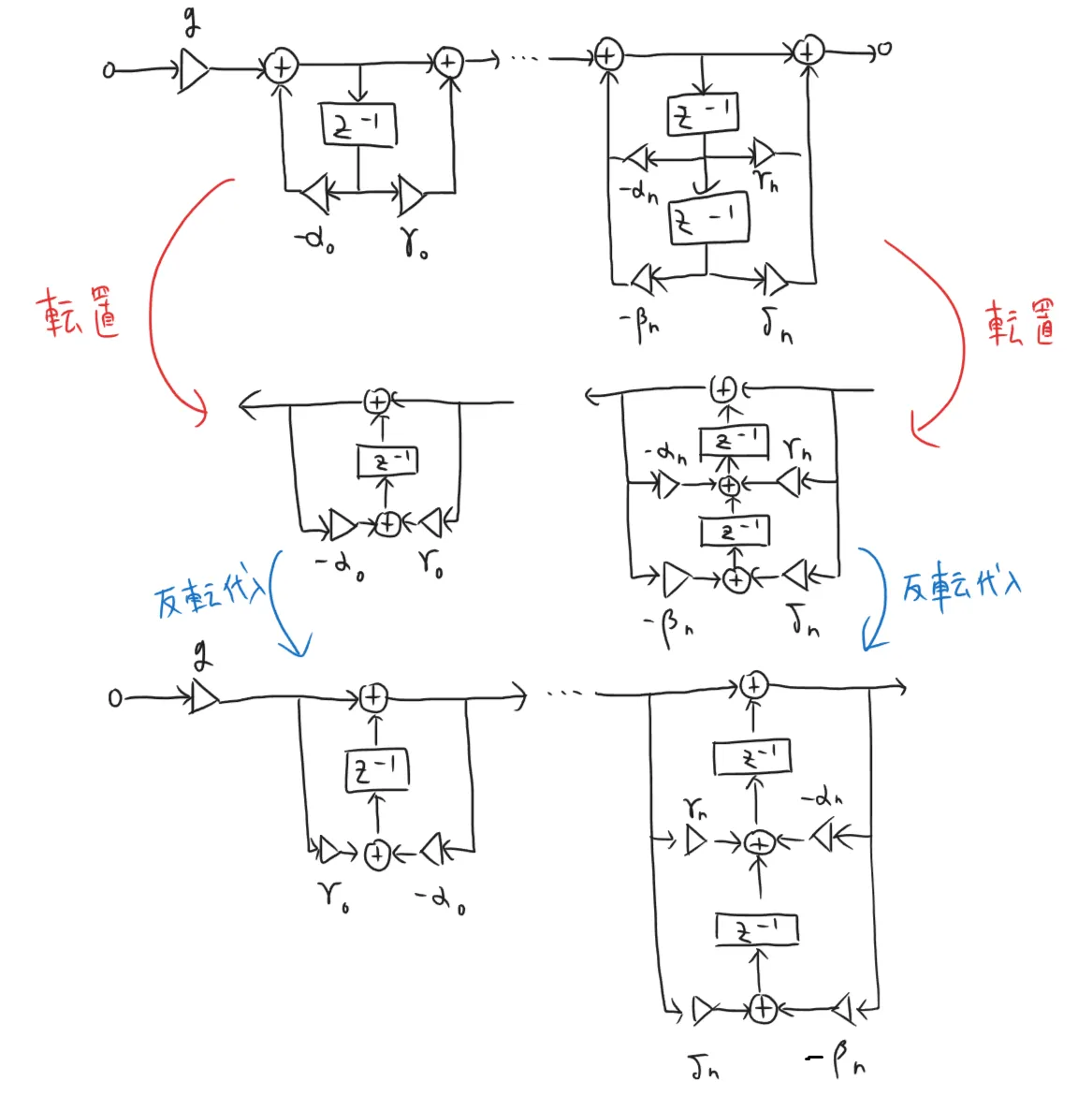
直接系Iの形を書き換える。加算の部分を境に2つに分割すれば、ブロックF F F G G G
伝達関数は有理関数で表されるので、これを1次や2次の縦続接続と見なせるように変形を行う。
Y ( z ) X ( z ) = ∑ k = 0 M a k z − k 1 + ∑ k = 1 N b k z − k = g 1 + γ 0 z − 1 1 + α 0 z − 1 ∏ i = 1 n 1 + γ i z − 1 + δ i z − 2 1 + a i z − 1 + β i z − 2 \begin{aligned}
\frac{Y(z)}{X(z)} &= \frac{\sum_{k=0}^{M} a_k z^{-k}}{1+\sum_{k=1}^{N} b_k z^{-k}} \\
&= g \frac{1+\gamma_0z^{-1}}{1+\alpha_0z^{-1}}\prod_{i=1}^n\frac{1+\gamma_iz^{-1}+\delta_iz^{-2}}{1+a_iz^{-1}+\beta_iz^{-2}}
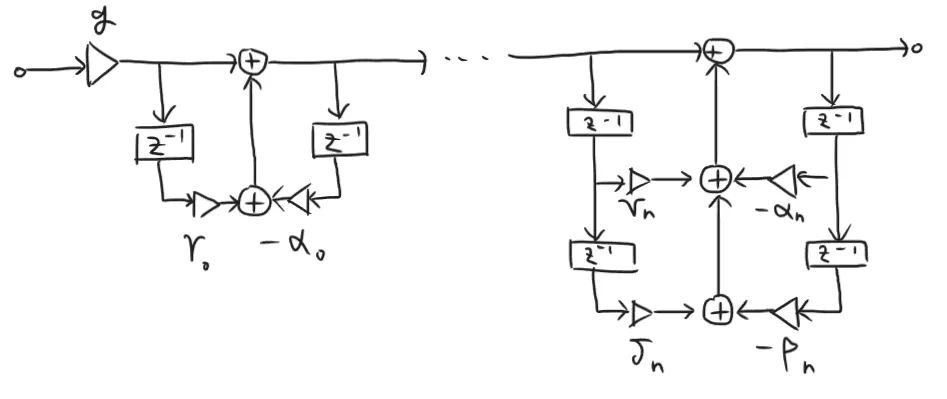
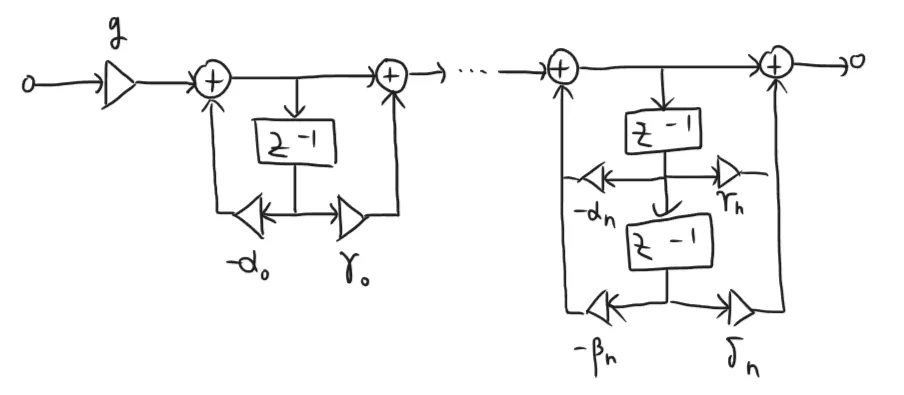
\end{aligned} X ( z ) Y ( z ) = 1 + ∑ k = 1 N b k z − k ∑ k = 0 M a k z − k = g 1 + α 0 z − 1 1 + γ 0 z − 1 i = 1 ∏ n 1 + a i z − 1 + β i z − 2 1 + γ i z − 1 + δ i z − 2 この変形により、2次以上の高次フィルタを1次や2次フィルタのカスケード接続に変換している。
これを直接形Iで書く。
直前に説明した構成を直接形IIで書く。
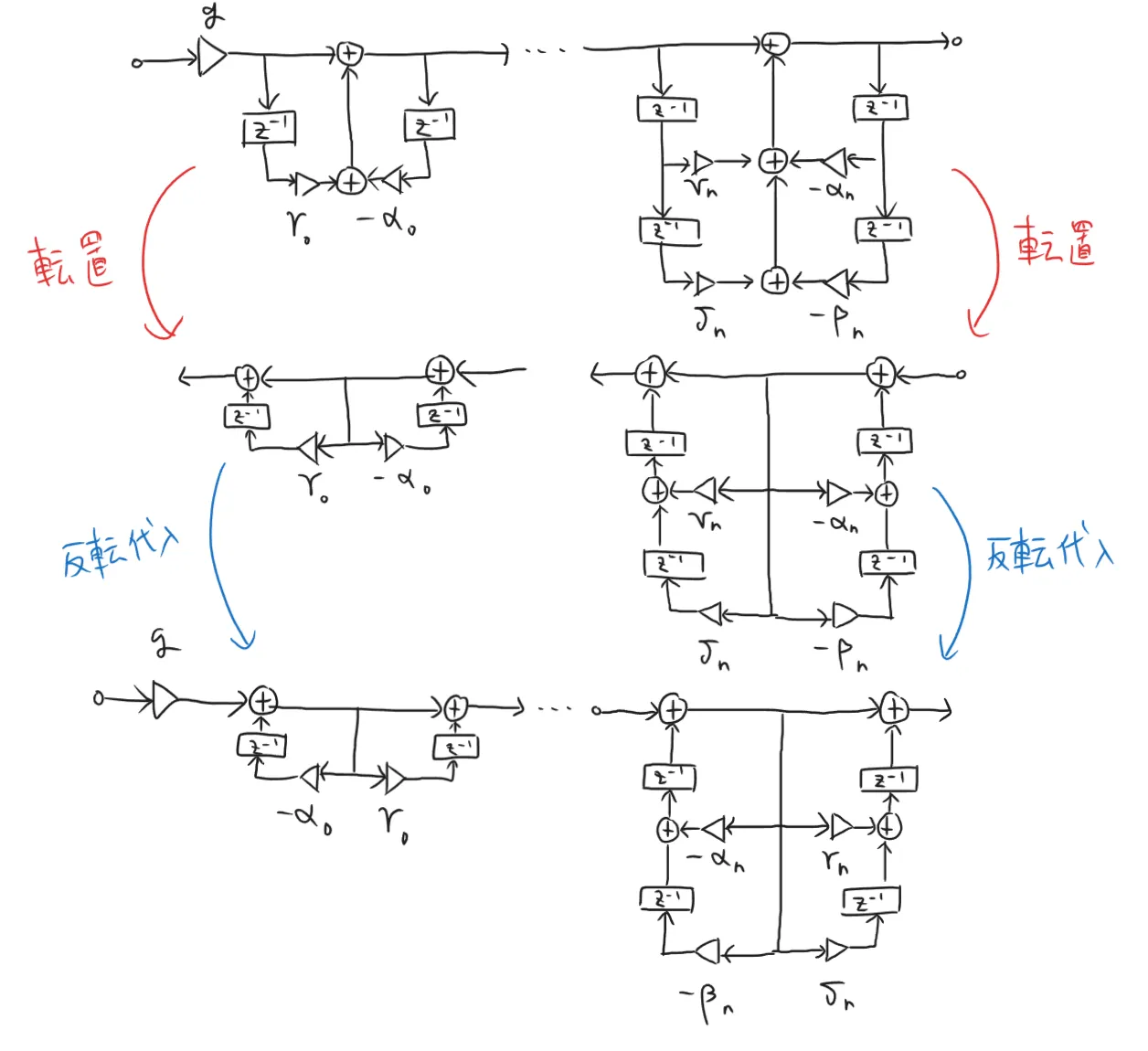
回路中の信号の向きを逆にし、加算器を信号の分岐で置き換えた回路を転置回路という。実は転置回路は元の回路と伝達関数が一致する。
プログラムに実装するとBiquad Direct Form IIと同じ実装になる。
同様に、Biquad Direct Form IIを転置する。
実験
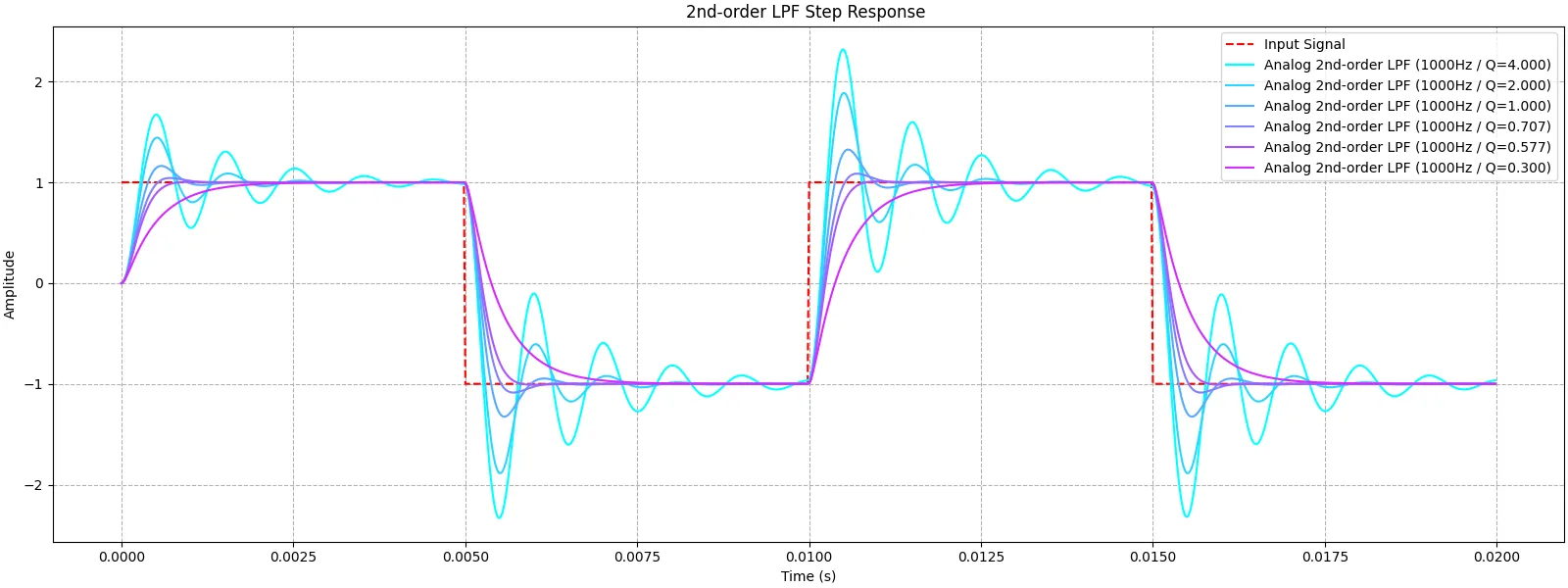
実験を行い、どのフィルタ構成が最も良いか確認する。題材となるフィルタは4次のピークフィルタとする。中心周波数をω c \omega_c ω c
H ( s ) = ( ω c 2 − s 2 s 2 + 2 R ω c s + ω c 2 ) 2 = s 4 − 2 ω c 2 s 2 + ω c 4 s 4 + 4 R ω c s 3 + ( 2 ω c 2 + 4 R 2 ω c 2 ) s 2 + 4 R ω c 3 s + ω c 4 \begin{aligned}
H(s) &= \left( \frac{\omega_c^2-s^2}{s^2+2R\omega_cs+\omega_c^2} \right)^2 \\
&= \frac{s^4-2\omega_c^2s^2+\omega_c^4}{s^4 + 4 R \omega_c s^3 + (2 \omega_c^2 + 4 R^2 \omega_c^2) s^2+ 4 R \omega_c^3 s + \omega_c^4}
\end{aligned} H ( s ) = ( s 2 + 2 R ω c s + ω c 2 ω c 2 − s 2 ) 2 = s 4 + 4 R ω c s 3 + ( 2 ω c 2 + 4 R 2 ω c 2 ) s 2 + 4 R ω c 3 s + ω c 4 s 4 − 2 ω c 2 s 2 + ω c 4 実験条件を単純にするために、双一次変換によりデジタルフィルタを得る。実験の際、カットオフ周波数はナイキスト周波数より十分低いものとする。
H ( z ) = ( ω c 2 T 2 − 4 4 + 4 R ω c T + ω c 2 T 2 + 2 ω c 2 T 2 + 8 4 + 4 R ω c T + ω c 2 T 2 z − 1 + ω c 2 T 2 − 4 4 + 4 R ω c T + ω c 2 T 2 z − 2 1 + − 8 + 2 ω c 2 T 2 4 + 4 R ω c T + ω c 2 T 2 z − 1 + 4 − 4 R ω c T + ω c 2 T 2 4 + 4 R ω c T + ω c 2 T 2 z − 2 ) 2 = a 0 + a 1 z − 1 + a 2 z − 2 1 + b 1 z − 1 + b 2 z − 2 ⋅ a 0 + a 1 z − 1 + a 2 z − 2 1 + b 1 z − 1 + b 2 z − 2 \begin{aligned}
H(z) &= \left( \frac{\frac{\omega_c^2T^2-4}{4+4R\omega_cT+\omega_c^2T^2} + \frac{2\omega_c^2T^2+8}{4+4R\omega_cT+\omega_c^2T^2}z^{-1}+\frac{\omega_c^2T^2-4}{4+4R\omega_cT+\omega_c^2T^2}z^{-2}}{1+\frac{-8+2\omega_c^2T^2}{4+4R\omega_cT+\omega_c^2T^2}z^{-1}+\frac{4-4R\omega_cT+\omega_c^2T^2}{4+4R\omega_cT+\omega_c^2T^2}z^{-2}} \right)^2 \\
&= \frac{a_0+a_1z^{-1}+a_2z^{-2}}{1+b_1z^{-1}+b_2z^{-2}}\cdot \frac{a_0+a_1z^{-1}+a_2z^{-2}}{1+b_1z^{-1}+b_2z^{-2}}
\end{aligned} H ( z ) = 1 + 4 + 4 R ω c T + ω c 2 T 2 − 8 + 2 ω c 2 T 2 z − 1 + 4 + 4 R ω c T + ω c 2 T 2 4 − 4 R ω c T + ω c 2 T 2 z − 2 4 + 4 R ω c T + ω c 2 T 2 ω c 2 T 2 − 4 + 4 + 4 R ω c T + ω c 2 T 2 2 ω c 2 T 2 + 8 z − 1 + 4 + 4 R ω c T + ω c 2 T 2 ω c 2 T 2 − 4 z − 2 2 = 1 + b 1 z − 1 + b 2 z − 2 a 0 + a 1 z − 1 + a 2 z − 2 ⋅ 1 + b 1 z − 1 + b 2 z − 2 a 0 + a 1 z − 1 + a 2 z − 2 直接形IとIIは次式のパラメータA 0 , A 1 , A 2 , A 3 , A 4 , B 1 , B 2 , B 3 , B 4 A_0, A_1, A_2, A_3, A_4, B_1, B_2, B_3, B_4 A 0 , A 1 , A 2 , A 3 , A 4 , B 1 , B 2 , B 3 , B 4
H ( z ) = a 0 + a 1 z − 1 + a 2 z − 2 1 + b 1 z − 1 + b 2 z − 2 ⋅ a 0 + a 1 z − 1 + a 2 z − 2 1 + b 1 z − 1 + b 2 z − 2 = a 0 2 + 2 a 0 a 1 z − 1 + ( 2 a 0 a 2 + a 1 2 ) z − 2 + 2 a 1 a 2 z − 3 + a 2 2 z − 4 1 + 2 b 1 z − 1 + ( 2 b 2 + b 1 2 ) z − 2 + 2 b 1 b 2 z − 3 + b 2 2 z − 4 = A 0 + A 1 z − 1 + A 2 z − 2 + A 3 z − 3 + A 4 z − 4 1 + B 1 z − 1 + B 2 z − 2 + B 3 z − 3 + B 4 z − 4 \begin{aligned}
H(z) &= \frac{a_0+a_1z^{-1}+a_2z^{-2}}{1+b_1z^{-1}+b_2z^{-2}}\cdot \frac{a_0+a_1z^{-1}+a_2z^{-2}}{1+b_1z^{-1}+b_2z^{-2}} \\
&= \frac{{a_0^2 + 2 a_0 a_1z^{-1} + (2 a_0 a_2 + a_1^2)z^{-2} + 2 a_1 a_2z^{-3} + a_2^2z^{-4}}}{{1 + 2 b_1z^{-1} + (2 b_2 + b_1^2)z^{-2} + 2 b_1 b_2z^{-3} + b_2^2z^{-4} }} \\
&= \frac{A_0+A_1z^{-1}+A_2z^{-2}+A_3z^{-3}+A_4z^{-4}}{1+B_1z^{-1}+B_2z^{-2}+B_3z^{-3}+B_4z^{-4}}
\end{aligned} H ( z ) = 1 + b 1 z − 1 + b 2 z − 2 a 0 + a 1 z − 1 + a 2 z − 2 ⋅ 1 + b 1 z − 1 + b 2 z − 2 a 0 + a 1 z − 1 + a 2 z − 2 = 1 + 2 b 1 z − 1 + ( 2 b 2 + b 1 2 ) z − 2 + 2 b 1 b 2 z − 3 + b 2 2 z − 4 a 0 2 + 2 a 0 a 1 z − 1 + ( 2 a 0 a 2 + a 1 2 ) z − 2 + 2 a 1 a 2 z − 3 + a 2 2 z − 4 = 1 + B 1 z − 1 + B 2 z − 2 + B 3 z − 3 + B 4 z − 4 A 0 + A 1 z − 1 + A 2 z − 2 + A 3 z − 3 + A 4 z − 4 Biquad DFI・IIとBiquad Transposed DFI・IIは次式のパラメータg , α 0 , β 0 , γ 0 , δ 0 , α 1 , β 1 , γ 1 , δ 1 g, \alpha_0, \beta_0, \gamma_0, \delta_0, \alpha_1, \beta_1, \gamma_1, \delta_1 g , α 0 , β 0 , γ 0 , δ 0 , α 1 , β 1 , γ 1 , δ 1
H ( z ) = a 0 + a 1 z − 1 + a 2 z − 2 1 + b 1 z − 1 + b 2 z − 2 ⋅ a 0 + a 1 z − 1 + a 2 z − 2 1 + b 1 z − 1 + b 2 z − 2 = a 0 2 1 + a 1 a 0 z − 1 + a 2 a 0 z − 2 1 + b 1 z − 1 + b 2 z − 2 ⋅ 1 + a 1 a 0 z − 1 + a 2 a 0 z − 2 1 + b 1 z − 1 + b 2 z − 2 = g 1 + γ 0 z − 1 + δ 0 z − 2 1 + α 0 z − 1 + β 0 z − 2 ⋅ 1 + γ 1 z − 1 + δ 1 z − 2 1 + α 1 z − 1 + β 1 z − 2 \begin{aligned}
H(z) &= \frac{a_0+a_1z^{-1}+a_2z^{-2}}{1+b_1z^{-1}+b_2z^{-2}}\cdot \frac{a_0+a_1z^{-1}+a_2z^{-2}}{1+b_1z^{-1}+b_2z^{-2}} \\
&= a_0^2 \frac{1+\frac{a_1}{a_0}z^{-1}+\frac{a_2}{a_0}z^{-2}}{1+b_1z^{-1}+b_2z^{-2}}\cdot \frac{1+\frac{a_1}{a_0}z^{-1}+\frac{a_2}{a_0}z^{-2}}{1+b_1z^{-1}+b_2z^{-2}} \\
&=g\frac{1+\gamma_0z^{-1}+\delta_0z^{-2}}{1+\alpha_0z^{-1}+\beta_0z^{-2}} \cdot \frac{1+\gamma_1z^{-1}+\delta_1z^{-2}}{1+\alpha_1z^{-1}+\beta_1z^{-2}}
\end{aligned} H ( z ) = 1 + b 1 z − 1 + b 2 z − 2 a 0 + a 1 z − 1 + a 2 z − 2 ⋅ 1 + b 1 z − 1 + b 2 z − 2 a 0 + a 1 z − 1 + a 2 z − 2 = a 0 2 1 + b 1 z − 1 + b 2 z − 2 1 + a 0 a 1 z − 1 + a 0 a 2 z − 2 ⋅ 1 + b 1 z − 1 + b 2 z − 2 1 + a 0 a 1 z − 1 + a 0 a 2 z − 2 = g 1 + α 0 z − 1 + β 0 z − 2 1 + γ 0 z − 1 + δ 0 z − 2 ⋅ 1 + α 1 z − 1 + β 1 z − 2 1 + γ 1 z − 1 + δ 1 z − 2 サンプリング周波数を48000Hzとし、中心周波数を20Hzと200Hz、R R R
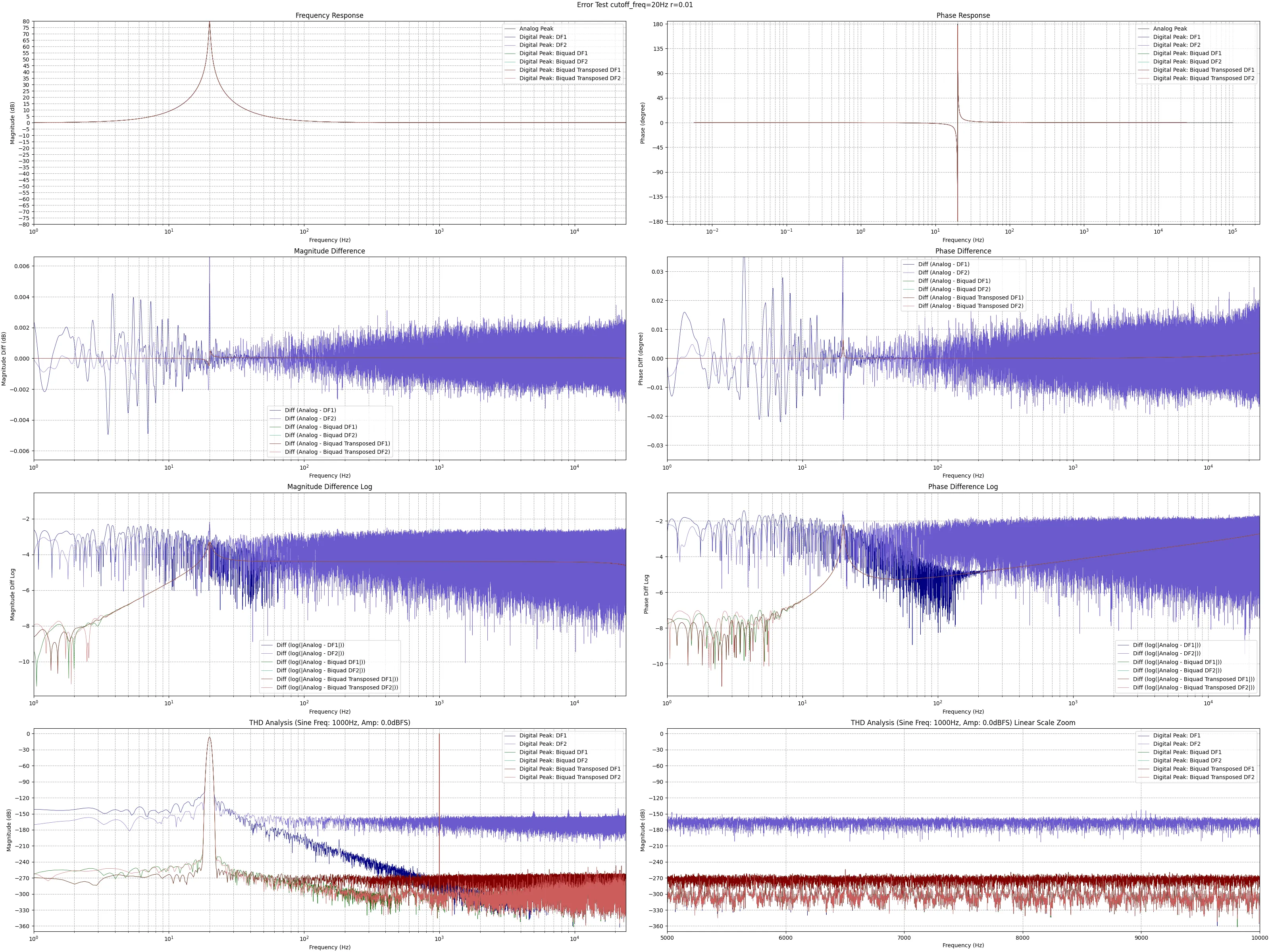
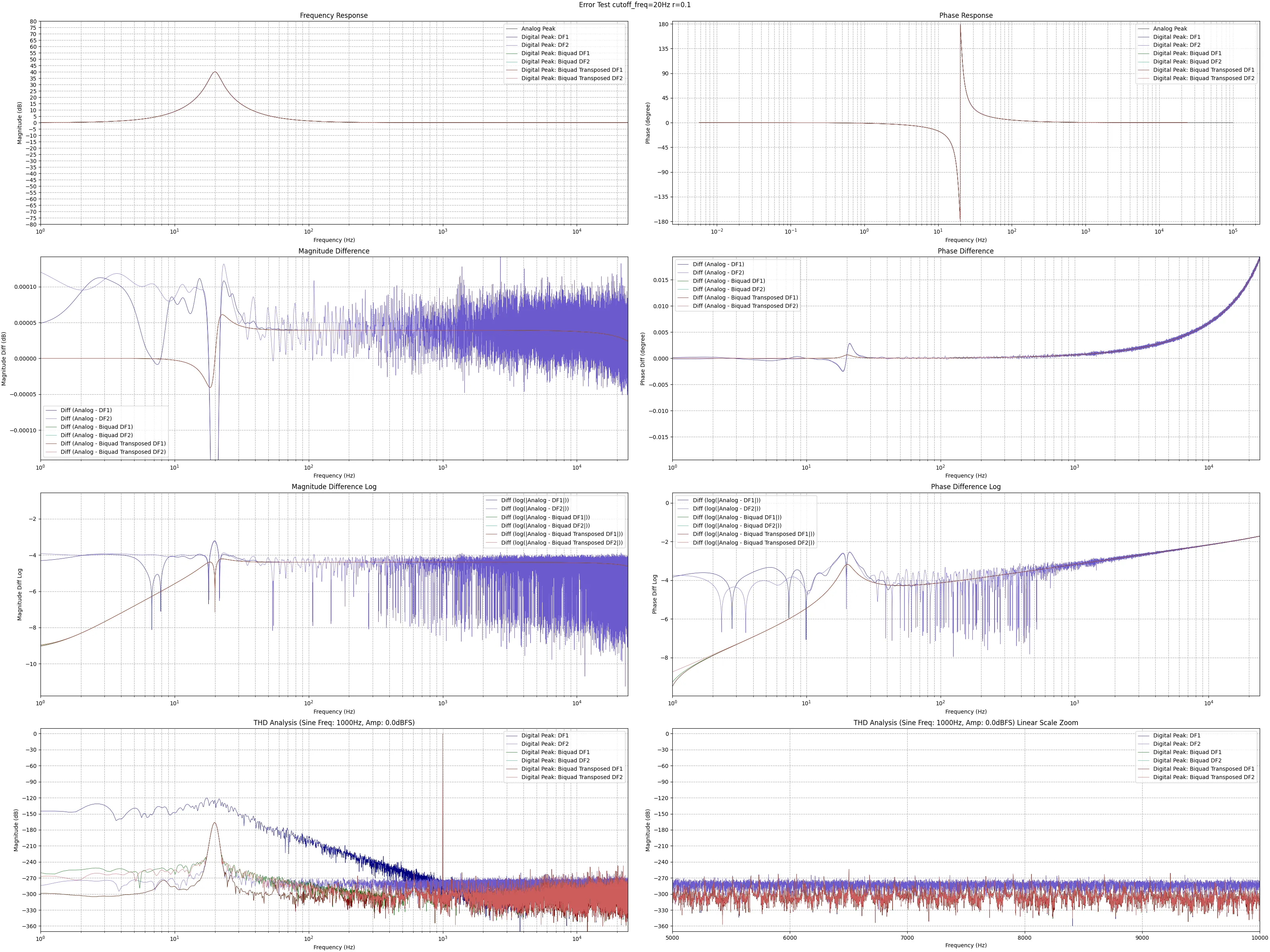
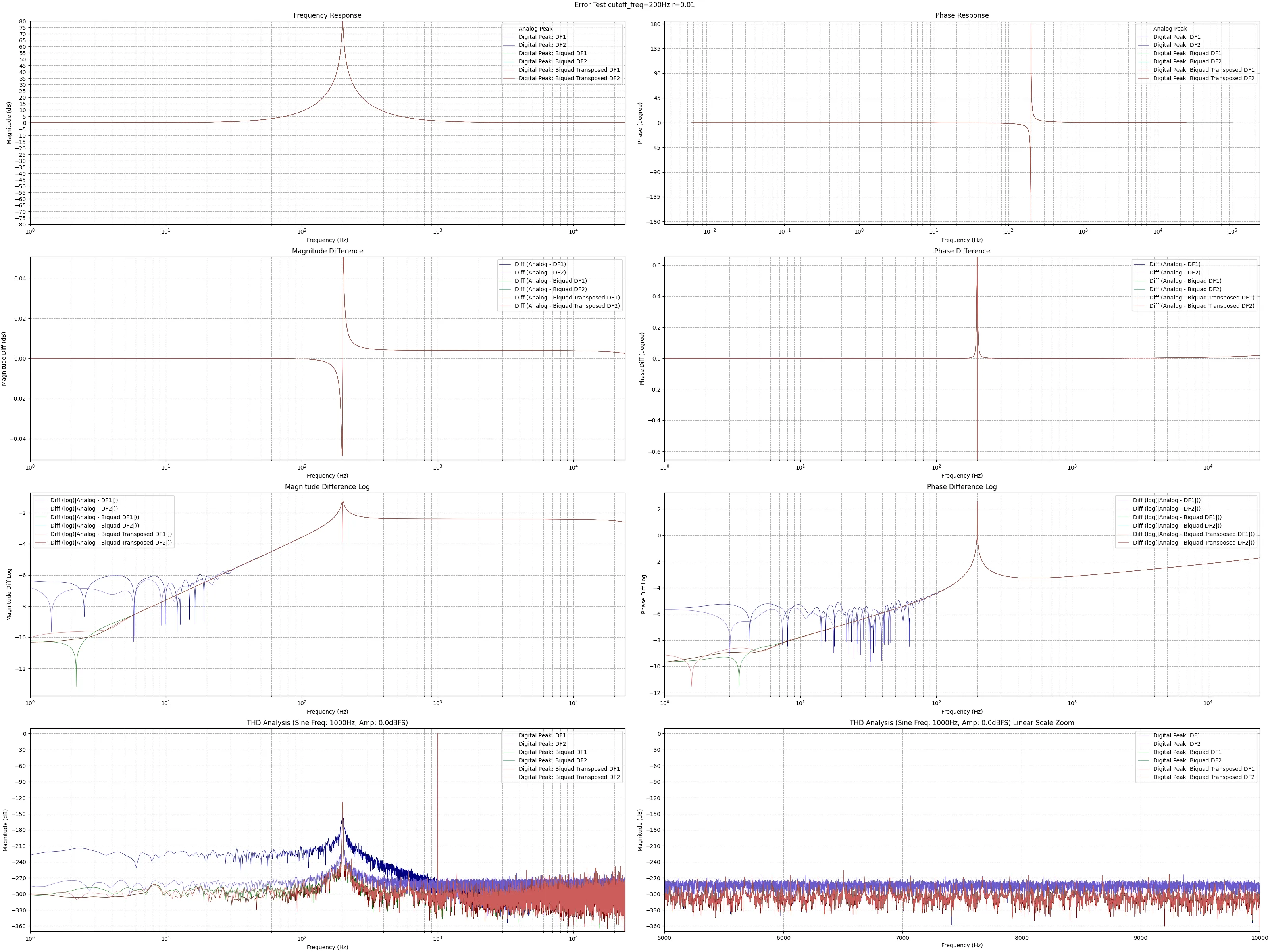
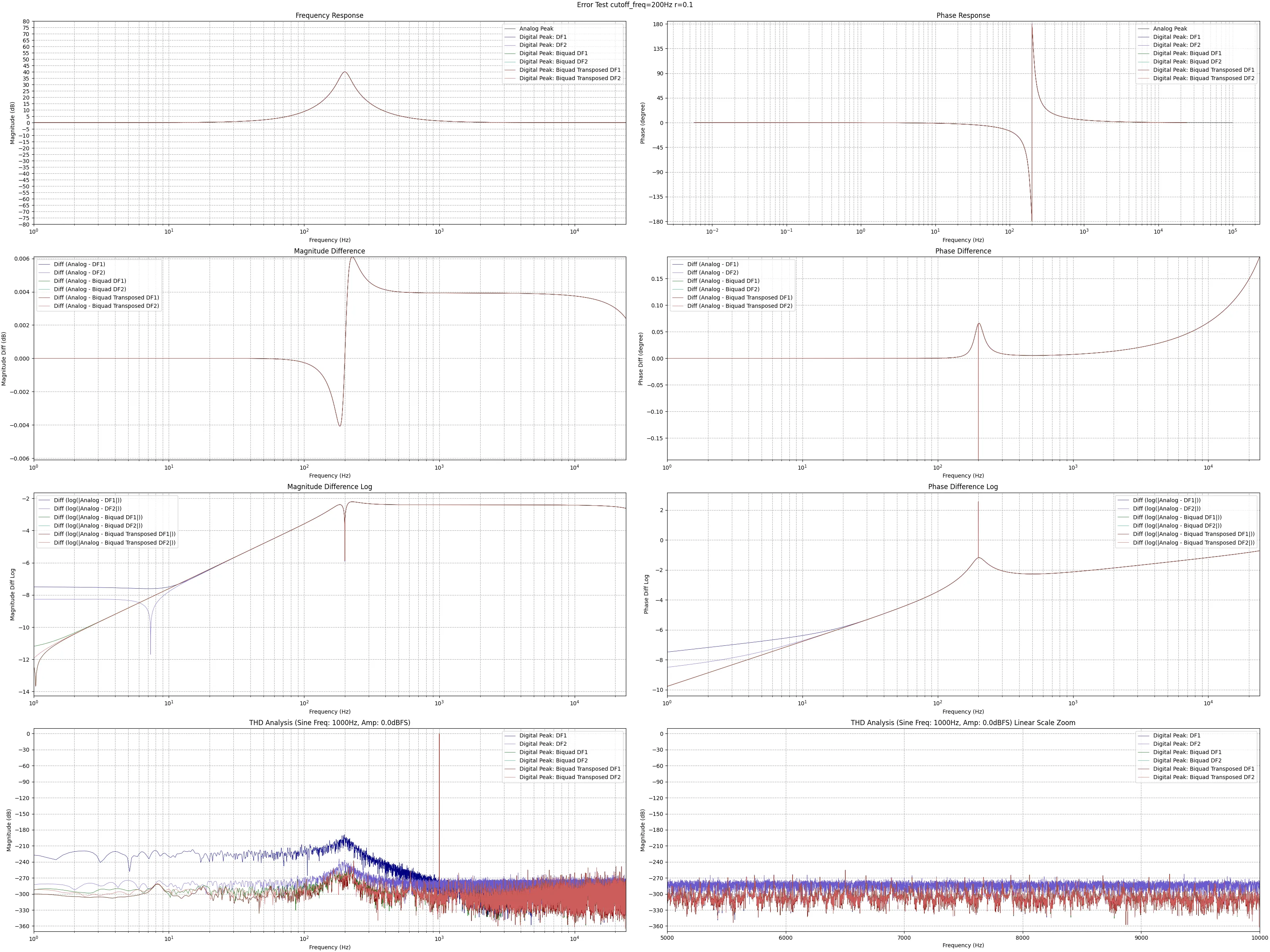
結果を下記に示す。上から3段目まで、左側のグラフが振幅特性、右側のグラフが位相特性を表す。各1段目のグラフが特性をそのまま示し、2段目のグラフは特性の差(Analog - Digital)、3段目のグラフは特性の差を対数表示したものである。4段目左右のグラフは1000Hz振幅0.0dBFSのサイン波を各実装に処理させ、結果の振幅特性を示した物である。2段目のグラフでは、プロットが0に近い程アナログフィルタと特性が近く、3段目のグラフでは、プロットが− ∞ -\infty − ∞ − ∞ -\infty − ∞
全体の傾向を見ると、
実装方法に関わらず、
中心周波数が高い方がアナログフィルタの特性を高精度に再現出来る
R R R
実装方法の優劣を判断すると
直接形(DFI・DFII)に比べて縦続形(Biquad○○)の方がアナログフィルタの特性再現度が高い
直接形(DFI・DFII)に比べて縦続形(Biquad○○)の方がTHD性能が良い
縦続形(Biquad○○)の中でも、Biquad DFIとBiquad Transposed DF2のTHD性能が良い
と分かる。
グラフ中にBiquad Direct Form IIが見えないが、Biquad Transposed Direct Form Iと完全に重なっている(同じ実装なため)。
サンプリング周波数を48000Hzとし、中心周波数f c = 20 [ H z ] f_c=20\ [\mathrm{Hz}] f c = 20 [ Hz ] R = 0.01 R=0.01 R = 0.01 f c = 200 [ H z ] f_c=200\ [\mathrm{Hz}] f c = 200 [ Hz ] R = 0.1 R=0.1 R = 0.1 f c f_c f c R R R
## f_c=20, R=0.01 ## 64bit float: T=0.000020833333333333333 1000bit float: T=0.000020833333333333333333... 64bit float: omega_c=125.66370614359172 1000bit float: omega_c=125.66370614359172953... 64bit float: b_0=4.000111573647065 1000bit float: b_0=4.0001115736470648607... 64bit float: a_0=-0.9999703939410614 1000bit float: a_0=-0.99997039394106147733... 64bit float: a_1=1.999947641582895 1000bit float: a_1=1.9999476415828950578... 64bit float: a_2=-0.9999703939410614 1000bit float: a_2=-0.99997039394106147733... 64bit float: b_1=-1.9999407878821227 1000bit float: b_1=-1.9999407878821229546... 64bit float: b_2=0.9999476415828948 1000bit float: b_2=0.99994764158289505784... 64bit float: A_0=0.9999407887586415 1000bit float: A_0=0.99994078875864168053... 64bit float: A_1=-3.9997768620302883 1000bit float: A_1=-3.999776862030288790... 64bit float: A_2=5.9996721465902665 1000bit float: A_2=5.9996721465902674341... 64bit float: A_3=-3.9997768620302883 1000bit float: A_3=-3.9997768620302887904... 64bit float: A_4=0.9999407887586415 1000bit float: A_4=0.99994078875864168053... 64bit float: B_1=-3.9998815757642454 1000bit float: B_1=-3.9998815757642459093... 64bit float: B_2=5.999658438200355 1000bit float: B_2=5.9996584382003568378... 64bit float: B_3=-3.99967214829633 1000bit float: B_3=-3.999672148296331671... 64bit float: B_4=0.9998952859071936 1000bit float: B_4=0.99989528590719395743... 64bit float: g=0.9999407887586415 1000bit float: g=0.99994078875864168053... 64bit float: alpha_0=-1.9999407878821227 1000bit float: alpha_0=-1.9999407878821229546... 64bit float: beta_0=0.9999476415828948 1000bit float: beta_0=0.99994764158289505784... 64bit float: gamma_0=-2.0000068539036895 1000bit float: gamma_0=-2.000006853903689179... 64bit float: delta_0=1.0 1000bit float: delta_0=1 64bit float: alpha_1=-1.9999407878821227 1000bit float: alpha_1=-1.9999407878821229546... 64bit float: beta_1=0.9999476415828948 1000bit float: beta_1=0.99994764158289505784... 64bit float: gamma_1=-2.0000068539036895 1000bit float: gamma_1=-2.000006853903689179... 64bit float: delta_1=1.0 1000bit float: delta_1=1 ## f_c=200, R=0.1 ## 64bit float: T=0.000020833333333333333 1000bit float: T=0.000020833333333333333333... 64bit float: omega_c=1256.6370614359173 1000bit float: omega_c=1256.6370614359172953... 64bit float: b_0=4.011157364706486 1000bit float: b_0=4.0111573647064860718... 64bit float: a_0=-0.9970475469236862 1000bit float: a_0=-0.99704754692368626323... 64bit float: a_1=1.9947785765753758 1000bit float: a_1=1.9947785765753758914... 64bit float: a_2=-0.9970475469236862 1000bit float: a_2=-0.99704754692368626323... 64bit float: b_1=-1.9940950938473725 1000bit float: b_1=-1.994095093847372526... 64bit float: b_2=0.9947785765753759 1000bit float: b_2=0.9947785765753758914... 64bit float: A_0=0.9941038108265403 1000bit float: A_0=0.99410381082654036092... 64bit float: A_1=-3.9777781728608024 1000bit float: A_1=-3.9777781728608023719... 64bit float: A_2=5.9673491912171635 1000bit float: A_2=5.9673491912171635009... 64bit float: A_3=-3.9777781728608024 1000bit float: A_3=-3.9777781728608023719... 64bit float: A_4=0.9941038108265403 1000bit float: A_4=0.99410381082654036092... 64bit float: B_1=-3.988190187694745 1000bit float: B_1=-3.988190187694745052... 64bit float: B_2=5.965972396456913 1000bit float: B_2=5.9659723964569132265... 64bit float: B_3=-3.9673661580268598 1000bit float: B_3=-3.9673661580268596909... 64bit float: B_4=0.9895844164133311 1000bit float: B_4=0.9895844164133309962... 64bit float: g=0.9941038108265403 1000bit float: g=0.99410381082654036092... 64bit float: alpha_0=-1.9940950938473725 1000bit float: alpha_0=-1.994095093847372526... 64bit float: beta_0=0.9947785765753759 1000bit float: beta_0=0.9947785765753758914... 64bit float: gamma_0=-2.0006855066542335 1000bit float: gamma_0=-2.0006855066542334901... 64bit float: delta_0=1.0 1000bit float: delta_0=1 64bit float: alpha_1=-1.9940950938473725 1000bit float: alpha_1=-1.994095093847372526... 64bit float: beta_1=0.9947785765753759 1000bit float: beta_1=0.9947785765753758914... 64bit float: gamma_1=-2.0006855066542335 1000bit float: gamma_1=-2.0006855066542334901... 64bit float: delta_1=1.0 1000bit float: delta_1=1 Chapter 4. アナログフィルタの伝達関数
Chapter 2.ではアナログフィルタの伝達関数H ( s ) H(s) H ( s ) H ( z ) H(z) H ( z ) H ( z ) H(z) H ( z ) H ( s ) H(s) H ( s )
とは言っても、アナログフィルタの伝達関数はインターネット上に多く落ちているため、必要があれば検索した方が早い。ここでは特に代表的な物を紹介するに留める。
アナログ1次フィルタ
Chapter 3.の実験結果から、高次のデジタルフィルタを作る際は1次か2次フィルタのカスケード接続をしたほうが性能が良いことを示した。似たようなことはアナログ回路でも言うことができ、高次のフィルタを作る際は低次のアクティブフィルタを多段縦続接続することが多い。
低域通過フィルタ
カットオフ周波数をω c \omega_c ω c
H L P F ( s ) = ω c s + ω c H_{\mathrm{LPF}}(s) = \frac{\omega_c}{s+\omega_c} H LPF ( s ) = s + ω c ω c 振幅特性は
∣ H L P F ( j ω ) ∣ = ω c ω 2 + ω c 2 |H_{\mathrm{LPF}}(j\omega)| = \frac{\omega_c}{\sqrt{\omega^2+\omega_c^2}} ∣ H LPF ( jω ) ∣ = ω 2 + ω c 2 ω c であり、カットオフ周波数の地点で振幅が1 2 \frac{1}{\sqrt{2}} 2 1 20 log 10 1 2 ≈ − 3.010 [ d B ] 20\log_{10}\frac{1}{\sqrt{2}}\approx-3.010\ [\mathrm{dB}] 20 log 10 2 1 ≈ − 3.010 [ dB ]
スロープは6dB/octである。
高域通過フィルタ
周波数対数スケール上で考えると、高域通過フィルタは低域通過フィルタの特性をω c \omega_c ω c s ω c → ω c s \frac{s}{\omega_c} \rightarrow \frac{\omega_c}{s} ω c s → s ω c
H H P F ( s ) = s s + ω c \begin{aligned}
H_{\mathrm{HPF}}(s) = \frac{s}{s+\omega_c}
\end{aligned} H HPF ( s ) = s + ω c s 振幅特性は
∣ H H P F ( j ω ) ∣ = ω ω 2 + ω c 2 |H_{\mathrm{HPF}}(j\omega)| = \frac{\omega}{\sqrt{\omega^2+\omega_c^2}} ∣ H HPF ( jω ) ∣ = ω 2 + ω c 2 ω であり、カットオフ周波数の地点で振幅が1 2 \frac{1}{\sqrt{2}} 2 1 20 log 10 1 2 ≈ − 3.010 [ d B ] 20\log_{10}\frac{1}{\sqrt{2}}\approx-3.010\ [\mathrm{dB}] 20 log 10 2 1 ≈ − 3.010 [ dB ]
スロープは6dB/octである。
低域シェルビングフィルタ
DC成分のゲインをA 0 A_0 A 0
H L S F ( s ) = s + A 0 ω c s + ω c H_{\mathrm{LSF}}(s) = \frac{s+A_0\omega_c}{s+\omega_c} H LSF ( s ) = s + ω c s + A 0 ω c 周波数特性は
∣ H L S F ( j ω ) ∣ = ω 2 + A 0 2 ω c 2 ω 2 + ω c 2 |H_{\mathrm{LSF}}(j\omega)| = \frac{\sqrt{\omega^2+A_0^2\omega_c^2}}{\sqrt{\omega^2+\omega_c^2}} ∣ H LSF ( jω ) ∣ = ω 2 + ω c 2 ω 2 + A 0 2 ω c 2 形が非対称であり、傾斜も選択できないためデジタルEQではあまり見かけない。
高域シェルビングフィルタ
低域通過フィルタから高域通過フィルタを求めたように、s ω c → ω c s \frac{s}{\omega_c} \rightarrow \frac{\omega_c}{s} ω c s → s ω c
H H S F ( s ) = A ∞ s + ω c s + ω c H_{\mathrm{HSF}}(s) = \frac{A_{\infty}s+\omega_c}{s+\omega_c} H HSF ( s ) = s + ω c A ∞ s + ω c を得る。A ∞ A_{\infty} A ∞
周波数特性は
∣ H H S F ( j ω ) ∣ = A ∞ 2 ω 2 + ω c 2 ω 2 + ω c 2 |H_{\mathrm{HSF}}(j\omega)| = \frac{\sqrt{A_{\infty}^2\omega^2+\omega_c^2}}{\sqrt{\omega^2+\omega_c^2}} ∣ H HSF ( jω ) ∣ = ω 2 + ω c 2 A ∞ 2 ω 2 + ω c 2 形が非対称であり、傾斜も選択できないためデジタルEQではあまり見かけない。
1次で実現できるのはこれで全て?
全て。
1次伝達関数の一般形を考えてみる。
H ( s ) = a 1 s + a 0 b 1 s + b 0 ∣ H ( j ω ) ∣ = a 1 2 ω 2 + a 0 2 b 1 2 ω 2 + b 0 2 H(s) = \frac{a_1s+a_0}{b_1s+b_0} \\
|H(j\omega)| = \frac{\sqrt{a_1^2\omega^2+a_0^2}}{\sqrt{b_1^2\omega^2+b_0^2}} H ( s ) = b 1 s + b 0 a 1 s + a 0 ∣ H ( jω ) ∣ = b 1 2 ω 2 + b 0 2 a 1 2 ω 2 + a 0 2 パラメータが多いので集約してみる。
a 1 = 0 a_1=0 a 1 = 0 H ( s ) = a 0 b 1 s + b 0 H(s)=\frac{a_0}{b_1s+b_0} H ( s ) = b 1 s + b 0 a 0
b 1 = 0 b_1=0 b 1 = 0 H ( s ) = a 0 b 0 H(s)=\frac{a_0}{b_0} H ( s ) = b 0 a 0 b 1 ≠ 0 b_1\neq0 b 1 = 0 H ( s ) = a 0 b 1 1 s + b 0 / b 1 H(s)=\frac{a_0}{b_1}\frac{1}{s+b_0/b_1} H ( s ) = b 1 a 0 s + b 0 / b 1 1
a 1 ≠ 0 a_1\neq0 a 1 = 0 a 1 a_1 a 1 H ( s ) = a 1 s + a 0 / a 1 b 1 s + b 0 H(s)=a_1\frac{s + a_0/a_1}{b_1s+b_0} H ( s ) = a 1 b 1 s + b 0 s + a 0 / a 1
b 1 = 0 b_1=0 b 1 = 0 H ( s ) = a 1 b 0 ( s + a 0 / a 1 ) H(s)=\frac{a_1}{b_0}(s + a_0/a_1) H ( s ) = b 0 a 1 ( s + a 0 / a 1 ) ∣ H ( j ω ) ∣ = a 1 b 0 ω 2 + a 0 2 a 1 2 |H(j\omega)|=\frac{a_1}{b_0}\sqrt{\omega^2+\frac{a_0^2}{a_1^2}} ∣ H ( jω ) ∣ = b 0 a 1 ω 2 + a 1 2 a 0 2
ω \omega ω
b 1 ≠ 0 b_1\neq0 b 1 = 0 H ( s ) = a 1 b 1 s + a 0 / a 1 s + b 0 / b 1 H(s)=\frac{a_1}{b_1}\frac{s+a_0/a_1}{s+b_0/b_1} H ( s ) = b 1 a 1 s + b 0 / b 1 s + a 0 / a 1
アナログ2次フィルタ
アナログ2次フィルタは、1次フィルタに比べると形とパラメータにバリエーションが出てくる。
低域通過フィルタ
カットオフ周波数をω c \omega_c ω c Q Q Q
H L P F ( s ) = ω c 2 s 2 + ω c Q s + ω c 2 H_{\mathrm{LPF}}(s) = \frac{\omega_c^2}{s^2+\frac{\omega_c}{Q}s+\omega_c^2} H LPF ( s ) = s 2 + Q ω c s + ω c 2 ω c 2 振幅特性は
∣ H L P F ( j ω ) ∣ = ω c 2 ( ω 2 − ω c 2 ) 2 + ω c 2 ω 2 Q 2 |H_{\mathrm{LPF}}(j\omega)| = \frac{\omega_c^2}{\sqrt{(\omega^2-\omega_c^2)^2+\frac{\omega_c^2\omega^2}{Q^2}}} ∣ H LPF ( jω ) ∣ = ( ω 2 − ω c 2 ) 2 + Q 2 ω c 2 ω 2 ω c 2
Q = 1 2 ≈ 0.707 Q=\frac{1}{\sqrt{2}}\approx0.707 Q = 2 1 ≈ 0.707 1 2 \frac{1}{\sqrt{2}} 2 1 20 log 10 1 2 ≈ − 3.010 [ d B ] 20\log_{10}\frac{1}{\sqrt{2}}\approx-3.010\ [\mathrm{dB}] 20 log 10 2 1 ≈ − 3.010 [ dB ]
また、Q = 1 3 ≈ 0.577 Q=\frac{1}{\sqrt{3}}\approx0.577 Q = 3 1 ≈ 0.577
Butterworth特性とは?
代表的なフィルタの特性(振幅特性の形)で、通過域の振幅特性が最大限平坦な特性のこと。
Butterworth特性は振幅特性の式で定義されており、低域通過フィルタが以下の特性を持つ物を指す。
∣ H ( j ω ) ∣ 2 = A 0 2 1 + ( ω ω c ) 2 n |H(j \omega)|^2 = \frac{A_0^2}{1+\left( \frac{\omega}{\omega_c} \right)^{2n}} ∣ H ( jω ) ∣ 2 = 1 + ( ω c ω ) 2 n A 0 2 A 0 A_0 A 0 n n n ∣ H L P F ( j ω ) ∣ 2 |H_{\mathrm{LPF}}(j\omega)|^2 ∣ H LPF ( jω ) ∣ 2 Q = 1 2 Q=\frac{1}{\sqrt{2}} Q = 2 1
∣ H L P F ( j ω ) ∣ 2 = ω c 4 ( ω 2 − ω c 2 ) 2 + 2 ω c 2 ω 2 = ω c 4 ω 4 − 2 ω c 2 ω 2 + ω c 4 + 2 ω c 2 ω 2 = ω c 4 ω 4 + ω c 4 = 1 1 + ( ω c ω ) 2 × 2 \begin{aligned}
|H_{\mathrm{LPF}}(j\omega)|^2 &= \frac{\omega_c^4}{(\omega^2-\omega_c^2)^2+2\omega_c^2\omega^2} \\
&= \frac{\omega_c^4}{\omega^4-2\omega_c^2\omega^2+\omega_c^4+2\omega_c^2\omega^2}\\
&= \frac{\omega_c^4}{\omega^4+\omega_c^4}\\
&= \frac{1}{1+\left(\frac{\omega_c}{\omega}\right)^{2\times2}}\\
\end{aligned} ∣ H LPF ( jω ) ∣ 2 = ( ω 2 − ω c 2 ) 2 + 2 ω c 2 ω 2 ω c 4 = ω 4 − 2 ω c 2 ω 2 + ω c 4 + 2 ω c 2 ω 2 ω c 4 = ω 4 + ω c 4 ω c 4 = 1 + ( ω ω c ) 2 × 2 1 となり、2次のButterworth特性を持つ。
Butterworth特性を持つn次LPFの伝達関数の有理関数を求めてみよう。∣ H ( j ω ) ∣ 2 |H(j \omega)|^2 ∣ H ( jω ) ∣ 2 H ( s ) H(s) H ( s ) s = j ω s=j\omega s = jω ∣ H ( j ω ) ∣ 2 = H ( j ω ) H ( j ω ) ‾ |H(j \omega)|^2 = H(j\omega)\overline{H(j \omega)} ∣ H ( jω ) ∣ 2 = H ( jω ) H ( jω )
∣ H ( j ω ) ∣ 2 = H ( j ω ) H ( j ω ) ‾ = A 0 2 1 + ( ω ω c ) 2 n H ( j ω ) H ( − j ω ) = A 0 2 1 + ( ω ω c ) 2 n H ( s ) H ( − s ) = A 0 2 1 + ( − j s ω c ) 2 n = A 0 2 1 + ( − s 2 ω c 2 ) n \begin{aligned}
|H(j \omega)|^2 = H(j\omega)\overline{H(j \omega)} &= \frac{A_0^2}{1+\left( \frac{\omega}{\omega_c} \right)^{2n}} \\
H(j\omega)H(-j\omega)&= \frac{A_0^2}{1+\left( \frac{\omega}{\omega_c} \right)^{2n}} \\
H(s)H(-s)&= \frac{A_0^2}{1+\left( \frac{-js}{\omega_c} \right)^{2n}} = \frac{A_0^2}{1+\left( \frac{-s^2}{\omega_c^2} \right)^{n}} \\
\end{aligned} ∣ H ( jω ) ∣ 2 = H ( jω ) H ( jω ) H ( jω ) H ( − jω ) H ( s ) H ( − s ) = 1 + ( ω c ω ) 2 n A 0 2 = 1 + ( ω c ω ) 2 n A 0 2 = 1 + ( ω c − j s ) 2 n A 0 2 = 1 + ( ω c 2 − s 2 ) n A 0 2 ここで、伝達関数がH ( s ) H ( − s ) H(s)H(-s) H ( s ) H ( − s )
1 + ( − s 2 ω c 2 ) n = 0 − s 2 ω c 2 = ( − 1 ) 1 n \begin{aligned}
1+\left( \frac{-s^2}{\omega_c^2} \right)^{n} &= 0\\
\frac{-s^2}{\omega_c^2} &= (-1)^{\frac{1}{n}}
\end{aligned} 1 + ( ω c 2 − s 2 ) n ω c 2 − s 2 = 0 = ( − 1 ) n 1 オイラーの公式から、
e j ( 2 k − 1 ) π = cos ( ( 2 k − 1 ) π ) + j sin ( ( 2 k − 1 ) π ) = − 1 ( k = 1 , 2 , 3 , ⋯ ) e^{j(2k-1)\pi}=\cos((2k-1)\pi)+j \sin((2k-1)\pi)=-1\quad (k=1,2,3,\cdots) e j ( 2 k − 1 ) π = cos (( 2 k − 1 ) π ) + j sin (( 2 k − 1 ) π ) = − 1 ( k = 1 , 2 , 3 , ⋯ ) なので、
− s 2 ω c 2 = ( − 1 ) 1 n = exp { j ( 2 k − 1 ) π n } − s 2 = ω c 2 exp { j ( 2 k − 1 ) π n } s 2 = ω c 2 exp { j ( 2 k − 1 ) π n } exp ( j π ) = ω c 2 exp { j ( 2 k + n − 1 ) π n } s = ω c exp { j ( 2 k + n − 1 ) π 2 n } \begin{aligned}
\frac{-s^2}{\omega_c^2} &= (-1)^{\frac{1}{n}} = \exp \left\{\frac{j(2k-1)\pi}{n} \right\} \\
-s^2 &= \omega_c^2 \exp\left\{\frac{j(2k-1)\pi}{n}\right\} \\
s^2 &= \omega_c^2 \exp \left\{\frac{j(2k-1)\pi}{n}\right\} \exp(j\pi) = \omega_c^2 \exp \left\{\frac{j(2k+n-1)\pi}{n} \right\} \\
s &= \omega_c \exp \left\{\frac{j(2k+n-1)\pi}{2n} \right\}
\end{aligned} ω c 2 − s 2 − s 2 s 2 s = ( − 1 ) n 1 = exp { n j ( 2 k − 1 ) π } = ω c 2 exp { n j ( 2 k − 1 ) π } = ω c 2 exp { n j ( 2 k − 1 ) π } exp ( jπ ) = ω c 2 exp { n j ( 2 k + n − 1 ) π } = ω c exp { 2 n j ( 2 k + n − 1 ) π } 最後に、得られた極を伝達関数H ( s ) H(s) H ( s ) H ( − s ) H(-s) H ( − s ) H ( s ) H(s) H ( s ) s s s k = 1 , 2 , 3 , ⋯ n k=1,2,3,\cdots n k = 1 , 2 , 3 , ⋯ n
以上より、H ( s ) H(s) H ( s )
H ( s ) = G 0 ∏ k = 1 n ω c s − s k ( k = 1 , 2 , 3 , ⋯ , n ) s k = ω c exp { j ( 2 k + n − 1 ) π 2 n } H(s) = G_0 \prod_{k=1}^n \frac{\omega_c}{s-s_k} \quad (k=1,2,3,\cdots, n) \\
s_k = \omega_c \exp \left\{\frac{j(2k+n-1)\pi}{2n} \right\} H ( s ) = G 0 k = 1 ∏ n s − s k ω c ( k = 1 , 2 , 3 , ⋯ , n ) s k = ω c exp { 2 n j ( 2 k + n − 1 ) π } 実際の極の位置は次のようになる。半径ω c \omega_c ω c
アナログフィルタもデジタルフィルタも、実装時は1次と2次フィルタの縦続接続を行うので、先ほど得たH ( s ) H(s) H ( s )
式を見やすくするため、周波数で正規化しs ω c → s \frac{s}{\omega_c} \rightarrow s ω c s → s
H ( s ) = G 0 ∏ k = 1 n 1 s − s k ( k = 1 , 2 , 3 , ⋯ , n ) s k = exp { j ( 2 k + n − 1 ) π 2 n } H(s) = G_0 \prod_{k=1}^n \frac{1}{s-s_k} \quad (k=1,2,3,\cdots, n) \\
s_k = \exp \left\{\frac{j(2k+n-1)\pi}{2n} \right\} H ( s ) = G 0 k = 1 ∏ n s − s k 1 ( k = 1 , 2 , 3 , ⋯ , n ) s k = exp { 2 n j ( 2 k + n − 1 ) π } 実軸対称の極をペアと考え、2次方程式の解と係数の関係を使えばH ( s ) H(s) H ( s ) B n ( s ) B_n(s) B n ( s )
B n ( s ) = { ∏ k = 1 n 2 ( s 2 − 2 s cos ( ( 2 k + n − 1 ) π 2 n ) + 1 ) ( n が偶数 ) ( s + 1 ) ∏ k = 1 n − 1 2 ( s 2 − 2 s cos ( ( 2 k + n − 1 ) π 2 n ) + 1 ) ( n が奇数 ) B_n(s) =
\begin{cases}
\prod_{k=1}^{\frac{n}{2}} (s^2 - 2s \cos \left( \frac{(2k+n-1)\pi}{2n} \right) + 1) & \quad (nが偶数) \\
(s+1)\prod_{k=1}^{\frac{n-1}{2}} (s^2 - 2s \cos \left( \frac{(2k+n-1)\pi}{2n} \right) + 1) & \quad (nが奇数) \\
\end{cases} B n ( s ) = ⎩ ⎨ ⎧ ∏ k = 1 2 n ( s 2 − 2 s cos ( 2 n ( 2 k + n − 1 ) π ) + 1 ) ( s + 1 ) ∏ k = 1 2 n − 1 ( s 2 − 2 s cos ( 2 n ( 2 k + n − 1 ) π ) + 1 ) ( n が偶数 ) ( n が奇数 )
このButterworth多項式を使えば、次数n n n
Bessel特性とは?
振幅特性はButterworthに似ているが、群遅延が最大平坦となる特性のこと。群遅延とは位相の周波数微分であり、要は位相の傾きのこと。位相の傾きが最大平坦ということは、最も線形位相に近いということである。
前に見せた周波数特性のグラフに、群遅延のグラフを追加すると次のようになる(3段目)。Q = 1 3 ≈ 0.577 Q=\frac{1}{\sqrt{3}}\approx0.577 Q = 3 1 ≈ 0.577
矩形波を入力した時の応答を見てみよう。こちらの方が分かりやすい。Q = 1 3 ≈ 0.577 Q=\frac{1}{\sqrt{3}}\approx0.577 Q = 3 1 ≈ 0.577
IIRデジタルフィルタでは線形位相を実現できない(※例外は次の補足を参照)。そのため、Bessel特性を持ったIIRフィルタは、線形位相に近い特性を実現したい時に大いに役に立つ。
Bessel特性を持つ低域通過フィルタの伝達関数は、Bessel多項式で表せる。具体的には、逆ベッセル多項式θ n ( s ) \theta_n(s) θ n ( s )
θ n ( s ) = ∑ k = 0 n ( n + k ) ! ( n − k ) ! k ! x n − k 2 k \theta_n(s) = \sum_{k=0}^n \frac{(n+k)!}{(n-k)!k!}\frac{x^{n-k}}{2^k} θ n ( s ) = k = 0 ∑ n ( n − k )! k ! ( n + k )! 2 k x n − k とし、
H n : B e s s e l : L P F ( s ) = θ n ( 0 ) θ n ( s / ω c ) H_{\mathrm{n:Bessel:LPF}}(s) = \frac{\theta_n(0)}{\theta_n(s/\omega_c)} H n : Bessel : LPF ( s ) = θ n ( s / ω c ) θ n ( 0 ) である。具体的にn = 2 n=2 n = 2
H 2 : B e s s e l : L P F ( s ) = 3 ω c 2 s 2 + 3 ω c s + 3 ω c 2 H_{\mathrm{2:Bessel:LPF}}(s) = \frac{3\omega_c^2}{s^2+3\omega_cs+3\omega_c^2} H 2 : Bessel : LPF ( s ) = s 2 + 3 ω c s + 3 ω c 2 3 ω c 2 になる。これはH L P F ( s ) H_{\mathrm{LPF}}(s) H LPF ( s ) Q = 1 3 Q=\frac{1}{\sqrt{3}} Q = 3 1 ω c \omega_c ω c H 2 : B e s s e l : L P F ( s ) H_{\mathrm{2:Bessel:LPF}}(s) H 2 : Bessel : LPF ( s ) H L P F ( s ) H_{\mathrm{LPF}}(s) H LPF ( s ) Q = 1 3 Q=\frac{1}{\sqrt{3}} Q = 3 1
H L P F ( s ) = ω c 2 s 2 + ω c 1 / 3 s + ω c 2 = ω c 2 s 2 + 3 ω c s + ω c 2 = ( 3 ω c , s c a l e d ) 2 s 2 + 3 ( 3 ω c , s c a l e d ) s + ( 3 ω c , s c a l e d ) 2 ※ ω c = 3 ω c , s c a l e d とスケール = 3 ω c , s c a l e d 2 s 2 + 3 ω c , s c a l e d s + 3 ω c , s c a l e d 2 \begin{aligned}
H_{\mathrm{LPF}}(s) &= \frac{\omega_c^2}{s^2+\frac{\omega_c}{1/\sqrt{3}}s+\omega_c^2} \\
&= \frac{\omega_c^2}{s^2+\sqrt{3}\omega_cs+\omega_c^2} \\
&= \frac{(\sqrt{3}\omega_{c,\ \mathrm{scaled}})^2}{s^2+\sqrt{3}(\sqrt{3}\omega_{c,\ \mathrm{scaled}})s+(\sqrt{3}\omega_{c,\ \mathrm{scaled}})^2} \quad \footnotesize ※\omega_c = \sqrt{3}\omega_{c,\ \mathrm{scaled}} とスケール \\
&= \frac{3\omega_{c,\ \mathrm{scaled}}^2}{s^2+3\omega_{c,\ \mathrm{scaled}}s+3\omega_{c,\ \mathrm{scaled}}^2}
\end{aligned} H LPF ( s ) = s 2 + 1/ 3 ω c s + ω c 2 ω c 2 = s 2 + 3 ω c s + ω c 2 ω c 2 = s 2 + 3 ( 3 ω c , scaled ) s + ( 3 ω c , scaled ) 2 ( 3 ω c , scaled ) 2 ※ ω c = 3 ω c , scaled とスケール = s 2 + 3 ω c , scaled s + 3 ω c , scaled 2 3 ω c , scaled 2 つまり、H L P F ( s ) H_{\mathrm{LPF}}(s) H LPF ( s ) Q = 1 3 Q=\frac{1}{\sqrt{3}} Q = 3 1 1000 × 1 3 ≈ 577 [ H z ] 1000 \times \frac{1}{\sqrt{3}} \approx 577\, [\mathrm{Hz}] 1000 × 3 1 ≈ 577 [ Hz ]
IIRで完璧な線形位相を得る方法
以下のような(トリッキーな)方法を使えば、IIRで線形位相を得られる。
与えられたサンプル列を通常のように順方向で処理をする。
処理後のサンプル列を反転する。
判定したサンプル列に順方向で処理をする。
処理後のサンプル列を反転する。
この方法をForward-Backwardと言ったりTIIRと言ったりする。順方向で処理した際に生じた位相変化は、逆方向で処理した時に打ち消されるので、結果的に線形位相になるわけだ。
一見魅力的な方法だが、DAWで動くVSTプラグインのように、ブロック単位でサンプル列が与えられる上にそこそこの時間で処理を終えないといけないシステムでは扱い勝手が悪い。
具体的な処理プロセスとして以下のような物が考えられるが、特に、前ブロックと加算する際に適切な処理を行わないとノイズの原因になる。また、仕組み上、フィルタ係数のオートメーション対応(サンプル単位での係数Rampingなど)を行いにくい。線形位相を得るだけならFIRフィルタ使った方が遥かに効率良く、実装もシンプルで、かつ同じ効果を得られるため、この手法を採用する意義は少ない。
Forward-BackwardとFIRのインパルス応答が全く同じ、つまりこの2つの手法が同じ動作であることを実際に確認してみる。IIRフィルタは下記の伝達関数を持つアナログピークフィルタを双一次変換でデジタルフィルタとする。このフィルタの伝達関数をH ( z ) H(z) H ( z ) R = 0.2 R=0.2 R = 0.2
H ( s ) = ω 0 2 − s 2 s 2 + 2 R ω 0 s + ω 0 2 H(s) = \frac{\omega_0^2-s^2}{s^2+2R\omega_0s+\omega_0^2} H ( s ) = s 2 + 2 R ω 0 s + ω 0 2 ω 0 2 − s 2 Forward-Backwardでは、同じフィルタを2回かけることになるので、その振幅特性は∣ H ( e j ω T ) ∣ × ∣ H ( e j ω T ) ∣ |H(e^{j\omega T})|\times|H(e^{j\omega T})| ∣ H ( e jω T ) ∣ × ∣ H ( e jω T ) ∣ 0 0 0 ∣ H ( e j ω T ) ∣ × ∣ H ( e j ω T ) ∣ |H(e^{j\omega T})|\times|H(e^{j\omega T})| ∣ H ( e jω T ) ∣ × ∣ H ( e jω T ) ∣
結果を以下に示す。左側1段目に、インパルス信号にIIRフィルタをForward-Backwardでかけて得たインパルス応答と、同じ特性を持つFIRフィルタのインパルス応答を示す。目視では差が分からないので、左側2段目に差を示す。差はなお小さいためdBFSで表示している。丁度DAWでNullテスト(片方を位相反転させて再生するやつ)を行った時のピークメータと思えば良い。右側1段目と2段目に周波数特性を示している。左側3段目には1000Hzのsin波に対して、Forward-BackwardとFIRの畳み込みを行った結果のTHDを示している。右側3段目は、左側3段目の結果を一部ズームして表示している。
結果から、Forward-Backwardのインパルス応答と、同じ特性を持つFIRフィルタのインパルス応答に殆ど差が無いことが分かる。差はdBFSで-250dB未満であり、知覚できない。更に、THDも特に変わらないことも分かる。
Forward-BackwardとFIRの畳み込みは、殆ど同じ結果が得られる。
高域通過フィルタ
物凄く寄り道してしまった。
周波数対数スケール上で考えると、高域通過フィルタは低域通過フィルタの特性をω c \omega_c ω c s ω c → ω c s \frac{s}{\omega_c} \rightarrow \frac{\omega_c}{s} ω c s → s ω c
H H P F ( s ) = s 2 s 2 + ω c Q s + ω c 2 H_{\mathrm{HPF}}(s) = \frac{s^2}{s^2+\frac{\omega_c}{Q}s+\omega_c^2} H HPF ( s ) = s 2 + Q ω c s + ω c 2 s 2 振幅特性は
∣ H H P F ( j ω ) ∣ = ω 2 ( ω 2 − ω c 2 ) 2 + ω c 2 ω 2 Q 2 |H_{\mathrm{HPF}}(j\omega)| = \frac{\omega^2}{\sqrt{(\omega^2-\omega_c^2)^2+\frac{\omega_c^2\omega^2}{Q^2}}} ∣ H HPF ( jω ) ∣ = ( ω 2 − ω c 2 ) 2 + Q 2 ω c 2 ω 2 ω 2 Q = 1 2 ≈ 0.707 Q=\frac{1}{\sqrt{2}}\approx0.707 Q = 2 1 ≈ 0.707 1 2 \frac{1}{\sqrt{2}} 2 1 20 log 10 1 2 ≈ − 3.010 [ d B ] 20\log_{10}\frac{1}{\sqrt{2}}\approx-3.010\ [\mathrm{dB}] 20 log 10 2 1 ≈ − 3.010 [ dB ]
また、Q = 1 3 ≈ 0.577 Q=\frac{1}{\sqrt{3}}\approx0.577 Q = 3 1 ≈ 0.577
帯域通過フィルタ
伝達関数は
H B P F ( s ) = ω c Q s s 2 + ω c Q s + ω c 2 H_{\mathrm{BPF}}(s) = \frac{\frac{\omega_c}{Q} s}{s^2+\frac{\omega_c}{Q}s+\omega_c^2} H BPF ( s ) = s 2 + Q ω c s + ω c 2 Q ω c s 振幅特性は
∣ H B P F ( j ω ) ∣ = ω c Q ω ( ω 2 − ω c 2 ) 2 + ω c 2 ω 2 Q 2 |H_{\mathrm{BPF}}(j\omega)| = \frac{\frac{\omega_c}{Q} \omega}{\sqrt{(\omega^2-\omega_c^2)^2+\frac{\omega_c^2\omega^2}{Q^2}}} ∣ H BPF ( jω ) ∣ = ( ω 2 − ω c 2 ) 2 + Q 2 ω c 2 ω 2 Q ω c ω 伝達関数をH B P F ( s ) = ω c s s 2 + ω c Q s + ω c 2 H_{\mathrm{BPF}}(s) = \frac{\omega_c s}{s^2+\frac{\omega_c}{Q}s+\omega_c^2} H BPF ( s ) = s 2 + Q ω c s + ω c 2 ω c s
このようなフィルタになっても、Q = 1 3 ≈ 0.577 Q=\frac{1}{\sqrt{3}}\approx0.577 Q = 3 1 ≈ 0.577
Notchフィルタ
帯域除去フィルタとも言う。
伝達関数は
H B R F ( s ) = s 2 + ω c 2 s 2 + ω c Q s + ω c 2 H_{\mathrm{BRF}}(s) = \frac{s^2 + \omega_c^2}{s^2+\frac{\omega_c}{Q}s+\omega_c^2} H BRF ( s ) = s 2 + Q ω c s + ω c 2 s 2 + ω c 2 振幅特性は
∣ H B R F ( j ω ) ∣ = ∣ − ω 2 + ω c 2 ∣ ( ω 2 − ω c 2 ) 2 + ω c 2 ω 2 Q 2 |H_{\mathrm{BRF}}(j\omega)| = \frac{|-\omega^2+\omega_c^2|}{\sqrt{(\omega^2-\omega_c^2)^2+\frac{\omega_c^2\omega^2}{Q^2}}} ∣ H BRF ( jω ) ∣ = ( ω 2 − ω c 2 ) 2 + Q 2 ω c 2 ω 2 ∣ − ω 2 + ω c 2 ∣ 位相特性のグラフを見ても分かる通り連続では無くなるため、Q = 1 3 ≈ 0.577 Q=\frac{1}{\sqrt{3}}\approx0.577 Q = 3 1 ≈ 0.577
全域通過フィルタ
伝達関数は
H A P F ( s ) = s 2 − ω c Q s + ω c 2 s 2 + ω c Q s + ω c 2 H_{\mathrm{APF}}(s) = \frac{s^2-\frac{\omega_c}{Q}s+\omega_c^2}{s^2+\frac{\omega_c}{Q}s+\omega_c^2} H APF ( s ) = s 2 + Q ω c s + ω c 2 s 2 − Q ω c s + ω c 2 振幅特性は
∣ H A P F ( j ω ) ∣ = 1 |H_{\mathrm{APF}}(j\omega)| = 1 ∣ H APF ( jω ) ∣ = 1
ピーキングフィルタ
ピークのゲインをA A A
伝達関数は
H P K F ( s ) = s 2 + A Q ω c s + ω c 2 s 2 + ω c Q A s + ω c 2 H_{\mathrm{PKF}}(s) = \frac{s^2+\frac{\sqrt{A}}{Q}\omega_cs+\omega_c^2}{s^2+\frac{\omega_c}{Q\sqrt{A}}s+\omega_c^2} H PKF ( s ) = s 2 + Q A ω c s + ω c 2 s 2 + Q A ω c s + ω c 2 振幅特性は
∣ H P K F ( j ω ) ∣ = ( ω 2 − ω c 2 ) 2 + A ω c 2 ω 2 Q 2 ( ω 2 − ω c 2 ) 2 + ω c 2 ω 2 A Q 2 |H_{\mathrm{PKF}}(j\omega)| = \frac{\sqrt{(\omega^2-\omega_c^2)^2+\frac{A\omega_c^2\omega^2}{Q^2}}}{\sqrt{(\omega^2-\omega_c^2)^2+\frac{\omega_c^2\omega^2}{AQ^2}}} ∣ H PKF ( jω ) ∣ = ( ω 2 − ω c 2 ) 2 + A Q 2 ω c 2 ω 2 ( ω 2 − ω c 2 ) 2 + Q 2 A ω c 2 ω 2
低域シェルビングフィルタ
伝達関数は
H L S F ( s ) = A s 2 + A 4 Q ω c s + ω c 2 A A s 2 + A 4 Q ω c s + ω c 2 H_{\mathrm{LSF}}(s) = \sqrt{A}\frac{s^2+\frac{\sqrt[4]{A}}{Q}\omega_cs+\omega_c^2\sqrt{A}}{\sqrt{A}s^2+\frac{\sqrt[4]{A}}{Q}\omega_cs+\omega_c^2} H LSF ( s ) = A A s 2 + Q 4 A ω c s + ω c 2 s 2 + Q 4 A ω c s + ω c 2 A 振幅特性は
∣ H L S F ( j ω ) ∣ = A ( ω 2 − ω c 2 A ) 2 + A Q 2 ω c 2 ω 2 ( A ω 2 − ω c 2 ) 2 + A Q 2 ω c 2 ω 2 |H_{\mathrm{LSF}}(j\omega)| = \sqrt{A}\frac{\sqrt{(\omega^2-\omega_c^2\sqrt{A})^2+\frac{\sqrt{A}}{Q^2}\omega_c^2\omega^2}}{\sqrt{(\sqrt{A}\omega^2-\omega_c^2)^2+\frac{\sqrt{A}}{Q^2}\omega_c^2\omega^2}} ∣ H LSF ( jω ) ∣ = A ( A ω 2 − ω c 2 ) 2 + Q 2 A ω c 2 ω 2 ( ω 2 − ω c 2 A ) 2 + Q 2 A ω c 2 ω 2 Q = 1 2 ≈ 0.707 Q=\frac{1}{\sqrt{2}}\approx0.707 Q = 2 1 ≈ 0.707
高域シェルビングフィルタ
伝達関数は
H H S F ( s ) = A A s 2 + A 4 Q ω c s + ω c 2 s 2 + A 4 Q ω c s + ω c 2 A H_{\mathrm{HSF}}(s) = \sqrt{A}\frac{\sqrt{A}s^2+\frac{\sqrt[4]{A}}{Q}\omega_cs+\omega_c^2}{s^2+\frac{\sqrt[4]{A}}{Q}\omega_cs+\omega_c^2\sqrt{A}} H HSF ( s ) = A s 2 + Q 4 A ω c s + ω c 2 A A s 2 + Q 4 A ω c s + ω c 2 振幅特性は
∣ H H S F ( j ω ) ∣ = A ( A ω 2 − ω c 2 ) 2 + A Q 2 ω c 2 ω 2 ( ω 2 − ω c 2 A ) 2 + A Q 2 ω c 2 ω 2 |H_{\mathrm{HSF}}(j\omega)| = \sqrt{A}\frac{\sqrt{(\sqrt{A}\omega^2-\omega_c^2)^2+\frac{\sqrt{A}}{Q^2}\omega_c^2\omega^2}}{\sqrt{(\omega^2-\omega_c^2\sqrt{A})^2+\frac{\sqrt{A}}{Q^2}\omega_c^2\omega^2}} ∣ H HSF ( jω ) ∣ = A ( ω 2 − ω c 2 A ) 2 + Q 2 A ω c 2 ω 2 ( A ω 2 − ω c 2 ) 2 + Q 2 A ω c 2 ω 2 Q = 1 2 ≈ 0.707 Q=\frac{1}{\sqrt{2}}\approx0.707 Q = 2 1 ≈ 0.707
アナログ高次フィルタ
HPFとLPFは高次フィルタが望まれる場面がある。そこで高次のデジタルフィルタを作るために1次か2次フィルタを単純に縦続接続すると、Qが同じなのにカットオフ周波数地点のゲインが変わってしまう。例えば3次のLPFを作る為に、下記の2つを縦続接続すると次のような結果が得られる。
H 1 , L P F ( s ) = ω c s + ω c H_{\mathrm{1,\ LPF}}(s) = \frac{\omega_c}{s+\omega_c} H 1 , LPF ( s ) = s + ω c ω c H 2 , L P F ( s ) = ω c 2 s 2 + ω c Q s + ω c 2 H_{\mathrm{2,\ LPF}}(s) = \frac{\omega_c^2}{s^2+\frac{\omega_c}{Q}s+\omega_c^2} H 2 , LPF ( s ) = s 2 + Q ω c s + ω c 2 ω c 2 H 3 , N a i v e L P F ( s ) = ω c s + ω c ⋅ ω c 2 s 2 + ω c Q s + ω c 2 H_{\mathrm{3,\ NaiveLPF}}(s) = \frac{\omega_c}{s+\omega_c} \cdot \frac{\omega_c^2}{s^2+\frac{\omega_c}{Q}s+\omega_c^2} H 3 , NaiveLPF ( s ) = s + ω c ω c ⋅ s 2 + Q ω c s + ω c 2 ω c 2
これはあまり望ましくない。そこで、Butterworth特性を基準にQを考え直してみる。「Butterworth特性とは」の項で説明したように、Butterworth多項式を使えば、LPFがButterworth特性を持つ時の分母の係数を知ることができる。
B n ( s ) = { ∏ k = 1 n 2 ( s 2 − 2 s cos ( ( 2 k + n − 1 ) π 2 n ) + 1 ) ( n が偶数 ) ( s + 1 ) ∏ k = 1 n − 1 2 ( s 2 − 2 s cos ( ( 2 k + n − 1 ) π 2 n ) + 1 ) ( n が奇数 ) B_n(s) =
\begin{cases}
\prod_{k=1}^{\frac{n}{2}} (s^2 - 2s \cos \left( \frac{(2k+n-1)\pi}{2n} \right) + 1) & \quad (nが偶数) \\
(s+1)\prod_{k=1}^{\frac{n-1}{2}} (s^2 - 2s \cos \left( \frac{(2k+n-1)\pi}{2n} \right) + 1) & \quad (nが奇数) \\
\end{cases} B n ( s ) = ⎩ ⎨ ⎧ ∏ k = 1 2 n ( s 2 − 2 s cos ( 2 n ( 2 k + n − 1 ) π ) + 1 ) ( s + 1 ) ∏ k = 1 2 n − 1 ( s 2 − 2 s cos ( 2 n ( 2 k + n − 1 ) π ) + 1 ) ( n が偶数 ) ( n が奇数 ) 3次Butterworth多項式はB 3 ( s ) = ( s + 1 ) ( s 2 + s + 1 ) B_3(s) = (s+1)(s^2+s+1) B 3 ( s ) = ( s + 1 ) ( s 2 + s + 1 )
H 3 , B u t t e r w o r t h L P F ( s ) = ω c s + ω c ⋅ ω c 2 s 2 + ω c s + ω c 2 H_{\mathrm{3,\ ButterworthLPF}}(s) = \frac{\omega_c}{s+\omega_c} \cdot \frac{\omega_c^2}{s^2+\omega_cs+\omega_c^2} H 3 , ButterworthLPF ( s ) = s + ω c ω c ⋅ s 2 + ω c s + ω c 2 ω c 2 である。H 2 , L P F ( s ) H_{\mathrm{2,\ LPF}}(s) H 2 , LPF ( s ) Q Q Q Q Q Q
H 3 , L P F ( s ) = ω c s + ω c ⋅ ω c 2 s 2 + ω c Q s + ω c 2 H_{\mathrm{3,\ LPF}}(s) = \frac{\omega_c}{s+\omega_c} \cdot \frac{\omega_c^2}{s^2+\frac{\omega_c}{Q}s+\omega_c^2} H 3 , LPF ( s ) = s + ω c ω c ⋅ s 2 + Q ω c s + ω c 2 ω c 2 を得る。H 3 , L P F ( s ) H_{\mathrm{3,\ LPF}}(s) H 3 , LPF ( s ) Q = 1 Q=1 Q = 1 H 2 , L P F ( s ) H_{\mathrm{2,\ LPF}}(s) H 2 , LPF ( s ) Q = 1 Q=1 Q = 1 B 2 ( s ) = s 2 + 2 s + 1 B_2(s) = s^2+\sqrt{2}s+1 B 2 ( s ) = s 2 + 2 s + 1
H 2 , L P F ( s ) = ω c 2 s 2 + 2 ω c Q s + ω c 2 H_{\mathrm{2,\ LPF}}(s) = \frac{\omega_c^2}{s^2+\sqrt{2}\frac{\omega_c}{Q}s+\omega_c^2} H 2 , LPF ( s ) = s 2 + 2 Q ω c s + ω c 2 ω c 2 と定義しなおせば、H 2 , L P F ( s ) H_{\mathrm{2,\ LPF}}(s) H 2 , LPF ( s ) Q = 1 Q=1 Q = 1 Q Q Q
4次以降の低域通過フィルタを作る時はQ Q Q
B 4 = ( s 2 − 2 s cos ( 5 8 π ) + 1 ) ( s 2 − 2 s cos ( 7 8 π ) + 1 ) B_4 = \left(s^2-2s \cos \left(\frac{5}{8}\pi\right)+1 \right)\left(s^2-2s \cos \left(\frac{7}{8}\pi\right)+1\right) B 4 = ( s 2 − 2 s cos ( 8 5 π ) + 1 ) ( s 2 − 2 s cos ( 8 7 π ) + 1 ) 4次Butterworth低域通過フィルタの伝達関数は、
H 4 , B u t t e r w o r t h L P F ( s ) = ω c 2 s 2 − 2 ω c s cos ( 5 8 π ) + ω c 2 ⋅ ω c 2 s 2 − 2 ω c s cos ( 7 8 π ) + ω c 2 H_{\mathrm{4,\ ButterworthLPF}}(s) = \frac{\omega_c^2}{s^2-2\omega_cs \cos \left(\frac{5}{8}\pi\right)+\omega_c^2} \cdot \frac{\omega_c^2}{s^2-2\omega_cs \cos \left(\frac{7}{8}\pi\right)+\omega_c^2} H 4 , ButterworthLPF ( s ) = s 2 − 2 ω c s cos ( 8 5 π ) + ω c 2 ω c 2 ⋅ s 2 − 2 ω c s cos ( 8 7 π ) + ω c 2 ω c 2 となる。Q Q Q k = 1 k=1 k = 1
H 4 , L P F ( s ) = ω c 2 s 2 − 2 ω c s cos ( 5 8 π ) Q + ω c 2 ⋅ ω c 2 s 2 − 2 ω c s cos ( 7 8 π ) + ω c 2 H_{\mathrm{4,\ LPF}}(s) = \frac{\omega_c^2}{s^2- \frac{2\omega_cs \cos \left(\frac{5}{8}\pi\right)}{Q}+\omega_c^2} \cdot \frac{\omega_c^2}{s^2-2\omega_cs \cos \left(\frac{7}{8}\pi\right)+\omega_c^2} H 4 , LPF ( s ) = s 2 − Q 2 ω c s c o s ( 8 5 π ) + ω c 2 ω c 2 ⋅ s 2 − 2 ω c s cos ( 8 7 π ) + ω c 2 ω c 2 同様にH 5 , L P F ( s ) H_{\mathrm{5,\ LPF}}(s) H 5 , LPF ( s ) H 6 , L P F ( s ) H_{\mathrm{6,\ LPF}}(s) H 6 , LPF ( s )
H 5 , L P F ( s ) = ω c s + ω c ⋅ ω c 2 s 2 − 2 ω c s cos ( 3 5 π ) Q + ω c 2 ⋅ ω c 2 s 2 − 2 ω c s cos ( 4 5 π ) + ω c 2 H 6 , L P F ( s ) = ω c 2 s 2 − 2 ω c s cos ( 7 12 π ) Q + ω c 2 ⋅ ω c 2 s 2 − 2 ω c s cos ( 3 4 π ) + ω c 2 ⋅ ω c 2 s 2 − 2 ω c s cos ( 11 12 π ) + ω c 2 \begin{aligned}
H_{\mathrm{5,\ LPF}}(s) &= \frac{\omega_c}{s+\omega_c} \cdot \frac{\omega_c^2}{s^2- \frac{2\omega_cs \cos \left(\frac{3}{5}\pi\right)}{Q}+\omega_c^2} \cdot \frac{\omega_c^2}{s^2-2\omega_cs \cos \left(\frac{4}{5}\pi\right)+\omega_c^2} \\
H_{\mathrm{6,\ LPF}}(s) &= \frac{\omega_c^2}{s^2- \frac{2\omega_cs \cos \left(\frac{7}{12}\pi\right)}{Q}+\omega_c^2} \cdot \frac{\omega_c^2}{s^2-2\omega_cs \cos \left(\frac{3}{4}\pi\right)+\omega_c^2} \cdot \frac{\omega_c^2}{s^2-2\omega_cs \cos \left(\frac{11}{12}\pi\right)+\omega_c^2}
\end{aligned} H 5 , LPF ( s ) H 6 , LPF ( s ) = s + ω c ω c ⋅ s 2 − Q 2 ω c s c o s ( 5 3 π ) + ω c 2 ω c 2 ⋅ s 2 − 2 ω c s cos ( 5 4 π ) + ω c 2 ω c 2 = s 2 − Q 2 ω c s c o s ( 12 7 π ) + ω c 2 ω c 2 ⋅ s 2 − 2 ω c s cos ( 4 3 π ) + ω c 2 ω c 2 ⋅ s 2 − 2 ω c s cos ( 12 11 π ) + ω c 2 ω c 2 図示すると次のようになる。Q Q Q Q Q Q
Q=1でButterworth特性を持つLPFでBessel特性を持つには?
元々のH 2 : L P F ( s ) H_{\mathrm{2:LPF}}(s) H 2 : LPF ( s ) Q = 1 3 Q=\frac{1}{\sqrt{3}} Q = 3 1
H 2 , o l d , L P F ( s ) = ω c 2 s 2 + ω c Q s + ω c 2 = ω c 2 s 2 + ω c 1 / 3 s + ω c 2 = ω c 2 s 2 + 3 ω c s + ω c 2 H_{\mathrm{2,\ old,\ LPF}}(s) = \frac{\omega_c^2}{s^2+\frac{\omega_c}{Q}s+\omega_c^2} = \frac{\omega_c^2}{s^2+\frac{\omega_c}{1/\sqrt{3}}s+\omega_c^2} = \frac{\omega_c^2}{s^2+\sqrt{3}\omega_cs+\omega_c^2} H 2 , old , LPF ( s ) = s 2 + Q ω c s + ω c 2 ω c 2 = s 2 + 1/ 3 ω c s + ω c 2 ω c 2 = s 2 + 3 ω c s + ω c 2 ω c 2 新たに定義したH 2 , L P F ( s ) H_{\mathrm{2,\ LPF}}(s) H 2 , LPF ( s ) s s s 3 \sqrt{3} 3 Q = 2 3 ≈ 0.8165 Q=\frac{\sqrt{2}}{\sqrt{3}}\approx0.8165 Q = 3 2 ≈ 0.8165
H 2 , L P F ( s ) = ω c 2 s 2 + 2 ω c 2 3 s + ω c 2 = ω c 2 s 2 + 2 3 2 ω c s + ω c 2 = ω c 2 s 2 + 3 ω c s + ω c 2 \begin{aligned}
H_{\mathrm{2,\ LPF}}(s) &= \frac{\omega_c^2}{s^2+\sqrt{2}\frac{\omega_c}{\frac{\sqrt{2}}{\sqrt{3}}}s+\omega_c^2} \\
&= \frac{\omega_c^2}{s^2+\sqrt{2}\frac{\sqrt{3}}{\sqrt{2}}\omega_cs+\omega_c^2} \\
&= \frac{\omega_c^2}{s^2+\sqrt{3}\omega_cs+\omega_c^2}
\end{aligned} H 2 , LPF ( s ) = s 2 + 2 3 2 ω c s + ω c 2 ω c 2 = s 2 + 2 2 3 ω c s + ω c 2 ω c 2 = s 2 + 3 ω c s + ω c 2 ω c 2 なお、3次以上のBessel特性を持つ低域通過フィルタはH n , L P F ( s ) H_{\mathrm{n,\ LPF}}(s) H n , LPF ( s ) Q Q Q
Chapter 5. まとめ
IIRなデジタルEQは
Chapter 4. を元にアナログフィルタの伝達関数H ( s ) H(s) H ( s )
Chapter 2. を元にH ( s ) H(s) H ( s ) H ( z ) H(z) H ( z )
Chapter 3. を元にプログラム実装
の手順で作ることができる。Chapter 2.~4. の背景知識としてChapter 1.の内容を使っている。
おすすめ文献
本記事を書くにあたって多くの本・サイトを参考にした。閲覧した中で特に役立ったものを下記に紹介する。
ディジタル信号処理システムの基礎 (森北出版 2008)
応用解析学の基礎 (森北出版 2014)
やる夫で学ぶディジタル信号処理
Vadim Zavalishin. The Art of VA Filter Design 2.1.2. (2020)
Robert Bristow-Johnson, Cookbook formulae for audio equalizer biquad filter coefficients
Introduction to Digital Filters: with Audio Applications (2007)

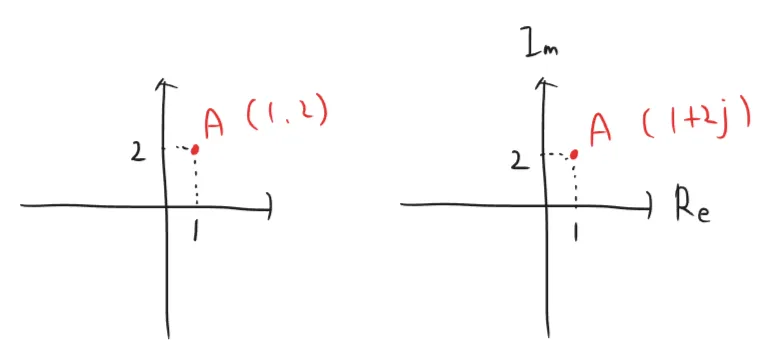
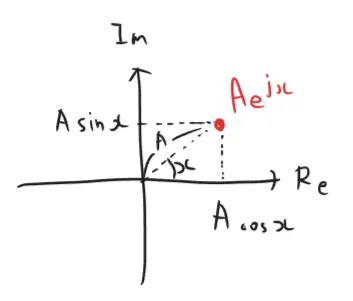
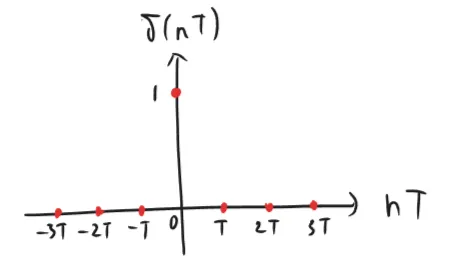

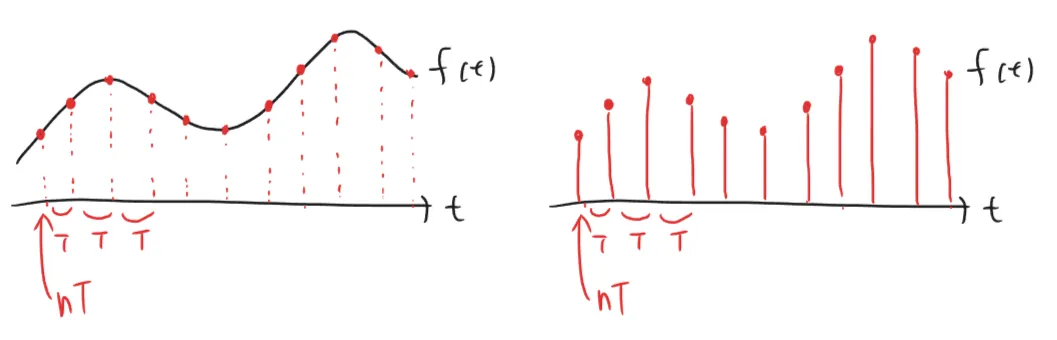
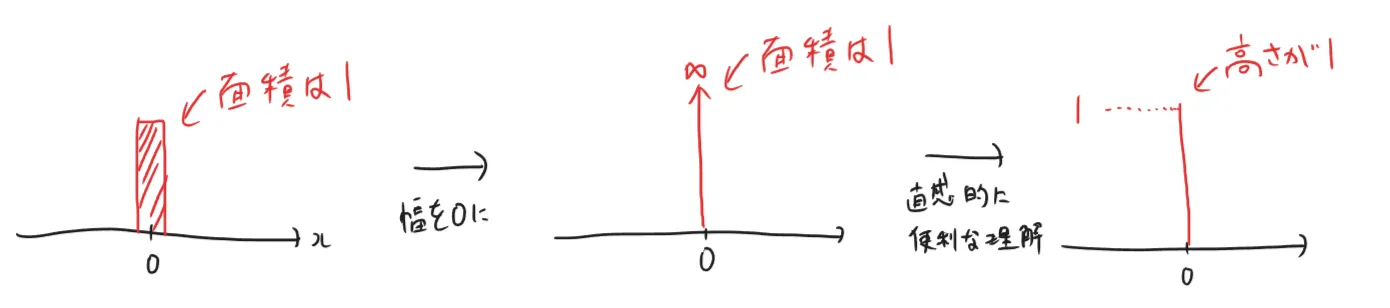
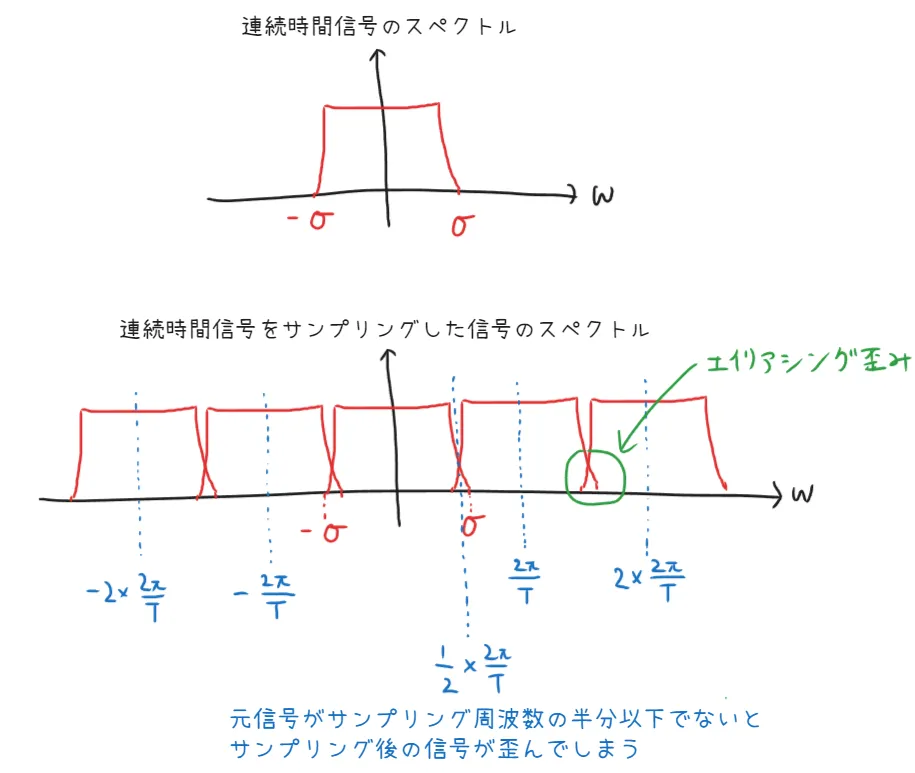
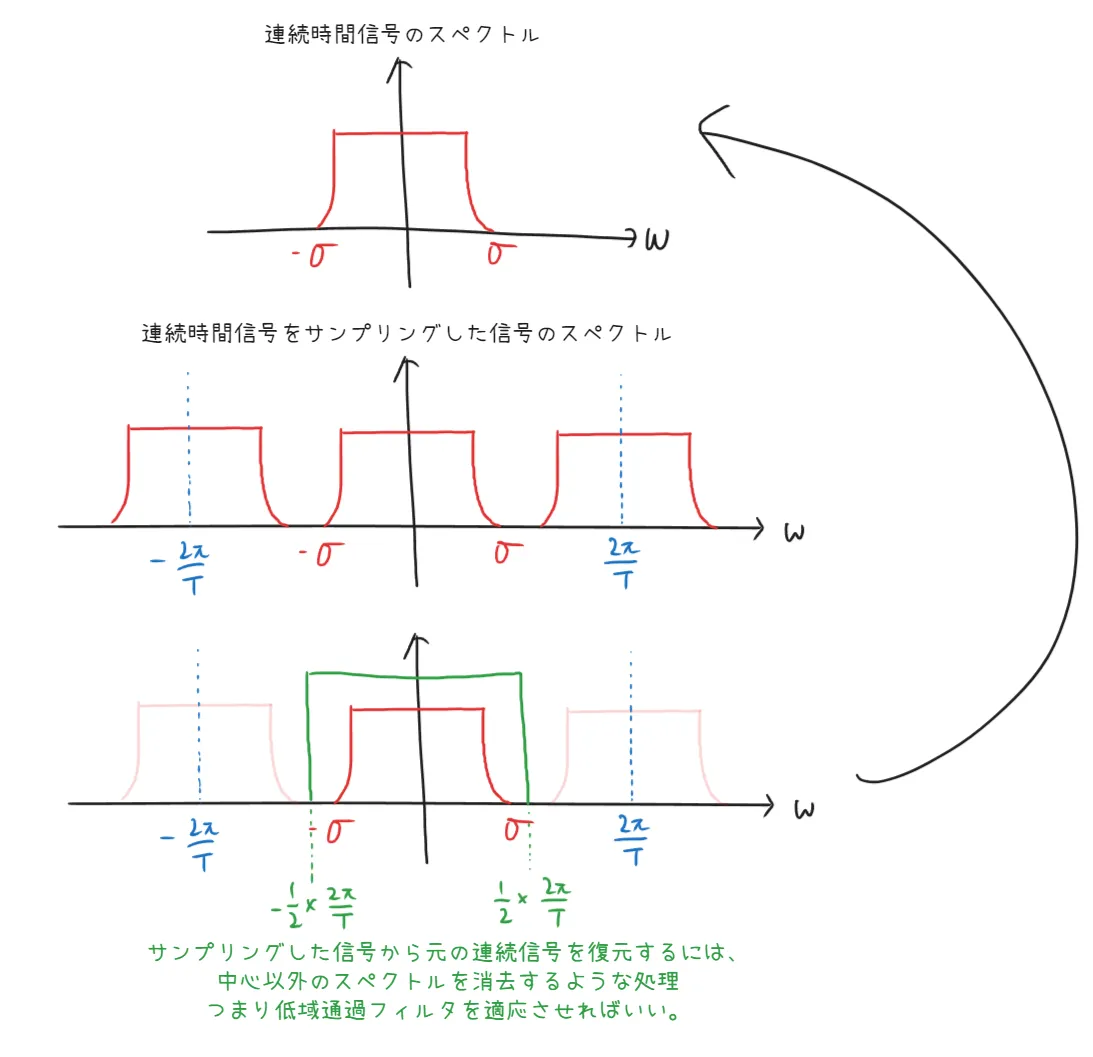
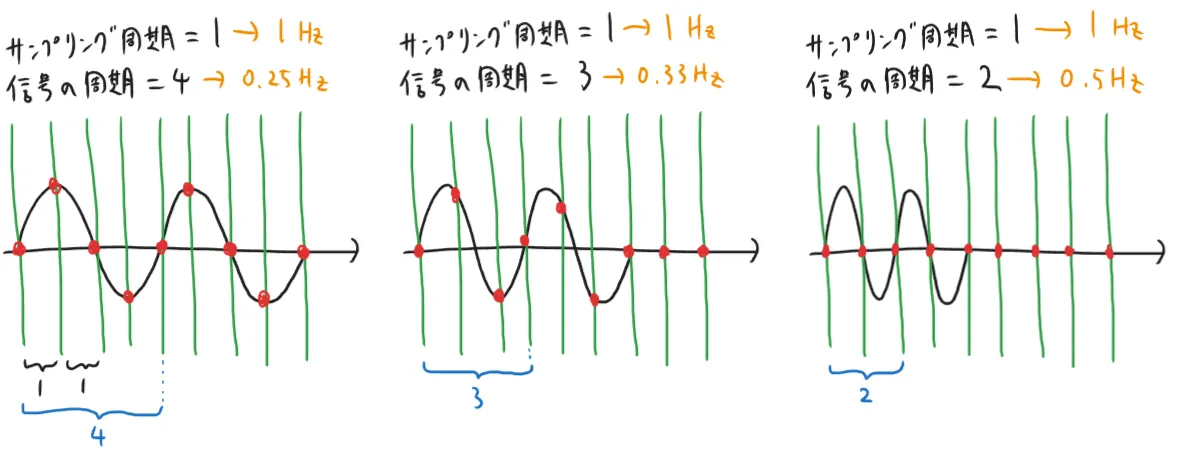
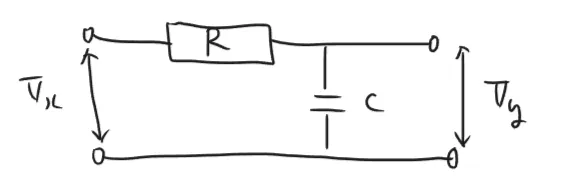
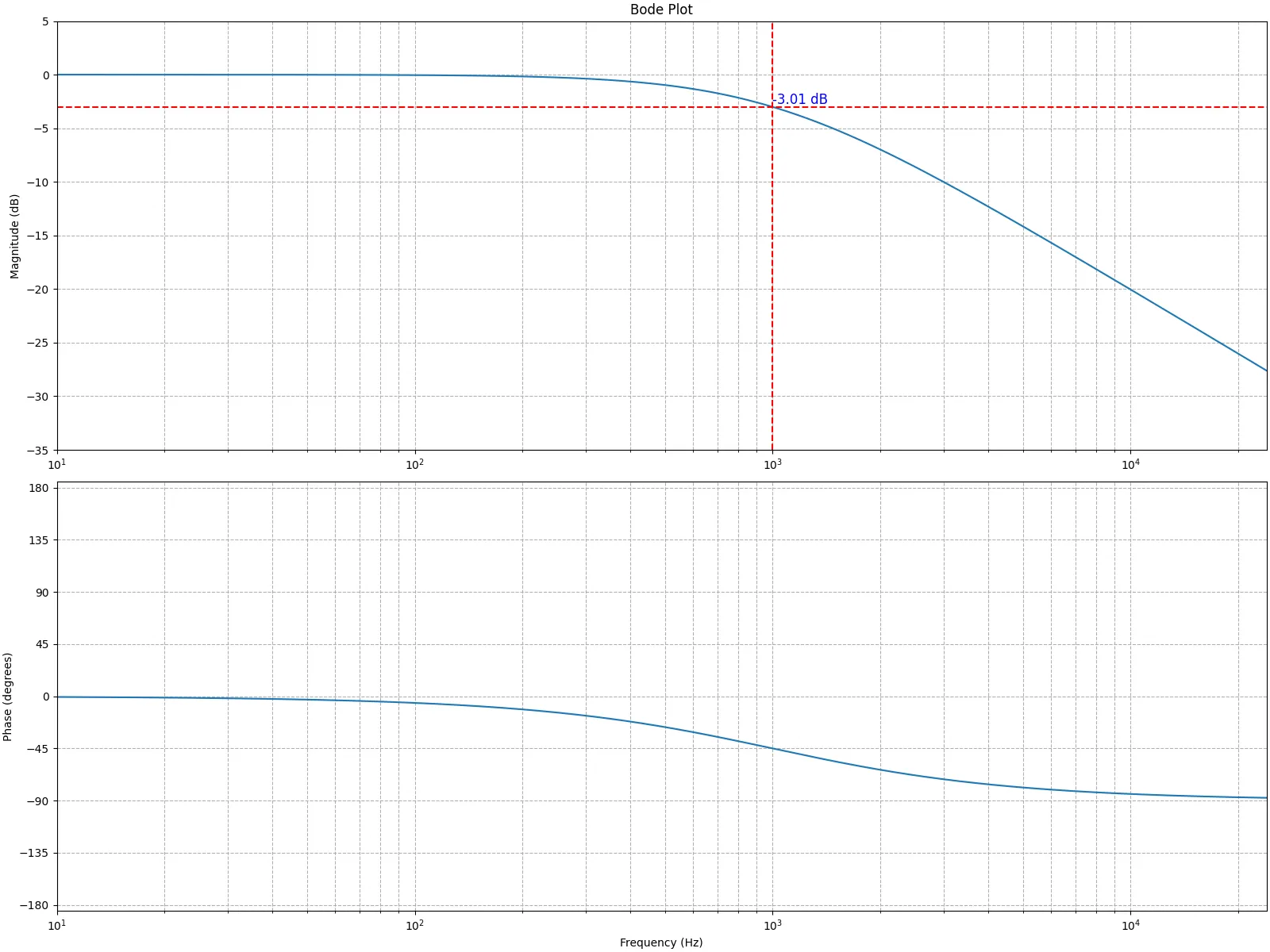
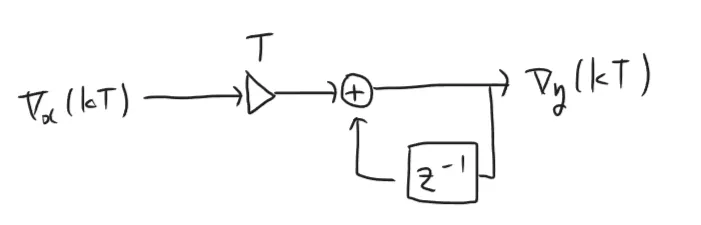 である。ここでとは信号を1サンプル遅らせるという意味である。
である。ここでとは信号を1サンプル遅らせるという意味である。